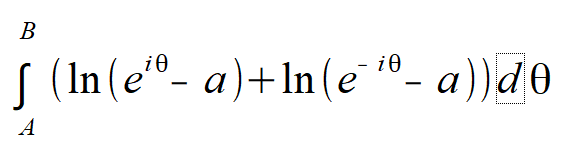Bonjour !
Il s'agit de calculer l'intégrale suivante :
J'ai la correction qui part à partir des sommes de Riemann du cos mais comme j'ai pas fait encore les sommes de Riemann j'aimerais bien avoir une autre solution... j'ai testé plusieurs changement de variables, la parité, etc. mais en vain.
Je me demande si l'intégrale est calculable par une autre méthode
Merci d'avance
Dernière modification par V13 ; 06/12/2017 à 16h41.
Je pense qu'il est possible de passer par une forme factorisé et de trouver la valeur en étudiant la limite, peut-être?
Au passage, ça n'est pas l'intégrale du Poisson, mais de Poisson. Du nom du mathématicien Siméon Denis Poisson
Bonjour Pour l'intégrale "de" Poisson on peut faire comme ceci:
On peut supposer que 0<a<1 , le calcul pour a>1 s'en déduira facilement.
On a
Avecon a
D'où
Il vient donc
Reste à déterminer c.
D'où
Bonjour,
la réponse ci-dessous n'est probablement pas celle attendue mais je tiens à la mentionner, ne serait-ce que pour son aspect "culturel".
Dans le langage de l'électrostatique bidimensionnelle, l'intégrale I est le potentiel électrique créé à une distance a de l'origine par une distribution uniforme de charge le long du cercle unité. Il est "bien connu" (utiliser soit votre version favorite de Stokes, soit des arguments géométriques élémentaires) que le champ électrique est nul à l'intérieur du cercle et coïncide à l'extérieur du cercle avec celui produit par une charge ponctuelle placée à l'origine. Cela suffit pour déterminer le potentiel à deux constantes additives près (une pour l'intérieur et l'autre pour l'extérieur), qui peuvent être déterminées en étudiant les cas faciles a=0 et a->+infini. En conclusion, I(a)=0 pour a entre 0 et 1, et I(a)=2 \pi log a pour a>1.
Bonjour @0577.
Ta remarque est très intéressante. En effet à cause des symétries le champ électrostatique est nul à l'intérieur du disque et on en déduit sans calcul (comme je l'ai fait) que le potentiel est nul à l'intérieur du disque. Autrement dit c'est un principe physique qui donne le résultat.
Pour le potentiel à l'extérieur (i.e pour a>1) l'intégrale se déduit très simplement de la valeur de l'intégrale pour (a<1). Ici c'est un calcul simple qui confirme que tout se passe comme si la charge était concentrée à l'origine.
J'ai alors une question:
Dans la cas a=1 le calcul (mathématique) n'est pas fait, mais est ce qu'il y a une explication physique qui conduirait au résultat?
Je suis bête, la continuité du potentiel! C'est bien cela??
