Suite et fonction Max: cas reel en entreprise

[vanhoa]

Bonjour a tous!

Je pose sur ce forum (Salon mathematique) car je ne savais pas trop si c’etait niveau Lycee ou Superieur. Ca fait quelques temps que je n’ai plus fait de maths (depuis ma prepa, soit 11 ans!!).
Je vais essayer de respecter au mieux les notations, excusez moi par avance si je fais des erreurs.
Je vais commencer par proposer mon debut de solution (car oui j’ai quand meme cherche avant) et je vous montrerai la ou je bloque.

Situation:
Une entreprise e-commerce recoit chaque jour des commandes clients a preparer et a envoyer (comme Amazon).
En debut de chaque journee, il peut parfois y avoir un certain nombre de commandes qui n’ont pas pu etre envoyees la veille, on appelle ca le “backlog”.
L'entreprise a une capacite d'envoi, c'est a dire un quantite maximale de commande qu'elle peut envoyer, elle est fixe.
Par exemple. Le jour i-1 j’ai recu 100 commandes, mais ma capacite maximale est 80, j’en ai donc envoye 80, et alors, le jour i j’ai 20 de backlog.
L'entreprise s'engage a envoye la commande au maximum 2 jours apres creation. Donc si un client fait une commande le Lundi, Mercredi au maximum, c'est envoye


Notations et remarques:
(l'editeur d'equation n'a pas l'air de marcher pour moi, j'en suis desole)
d_i = la quantite de nouvelles commande le jour i (d_i > ou = 0)
B_i = le backlog au jour i (B_i > ou = 0)
B₀ = 0 effectivement, il n'y a pas de backlog le premier jour
Q_i = la quantite de commandes a envoyer le jour i
C = la capacite, la quantite maximale de commandes que l'entreprise peut envoyer par jour (C>0)

On a donc les relations suivantes:
B_i = max(Q_i-1-C ; 0) effectivement, le backlog du jour i c'est le maximum entre la quantite de commandes qu'on devait traiter le jour precedent moins la capacite et zero!
Q_i = d_i+B_i
= d_i+max(Q_i-1-C ; 0)
= max(Q_i-1+d_i-C ; d_i)

_bQuestion_/b:
quelle est, en fonction des d_i, la capacite minimale C necessaire pour respecter l'engagement d'envoyer une commande au plus tard 2 jours apres jour de creation?

Mon debut de solution:

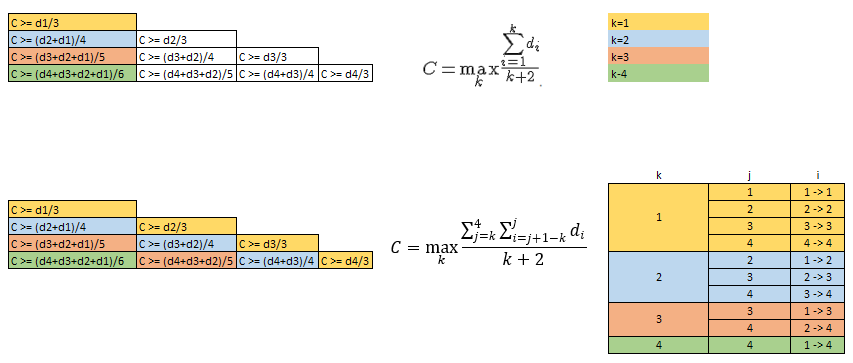
En gros, il faut que chaque Q_i soit < ou = a 3C:
Q_i = max(Q_i-1+d_i-C ; d_i) <= 3C
On a donc une suite Q_i

La facon dont j'ai procede est de commencer par Q₀, puis Q₁ etc... pour voir si on pouvait generaliser une formule a Q_n. Je trouve une relation qui peut se demontrer facilement par recurrence:

Q_n = max(d_n+d_n-1+...+d₁-(n-1)C ; d_n+d_n-1+...+d₂-(n-2)C ; ... ; d_n+d_n-1-C ; d_n)
Je mets en piece jointe l'image de l'equation pour que ce soit plus lisible.



c'est donc une fonction max avec n termes a comparer:
1er terme: d_n+d_n-1+...+d₁-(n-1)C
2eme terme: d_n+d_n-1+...+d₂-(n-2)C
...
n-1eme terme: d_n+d_n-1-C
neme terme: d_n

Sachant ca il faut ensuite comparer chaque Q_i a 3 fois la capacite C:
Q₁<=3C
Q₂<=3C
...
Q_n<=3C
pour respecter l'engagement il faut donc prendre la maximum de ces Q_i, ainsi, l'engagement sera toujours respecte.
Mais je coince, j'ai exprime mon Q_n mais je ne sais pas comment trouver mon C en fonction des d_i.

Merci de votre aide!!

Vanhoa
-----

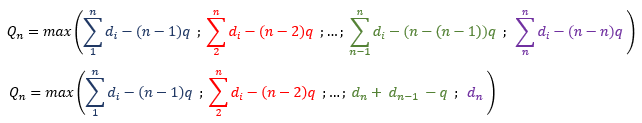
[vanhoa]

Excusez moi, dans l'image de l'equation j'ai mis "q" au lieu de "C", ca devrait etre:

[gg0]

Bonjour.

Ton problème est bien posé au niveau des notations, mais je m'interroge sur la réalité d'une solution algébrique : Sauf erreur, tu ne maîtrises pas les valeurs d_i et si l'une d'entre elles est supérieure à 3C, l'envoi en moins de 2 jours ne sera pas possible, sauf embauche de personnel supplémentaire.

En général (*), ce type de questions est traitée par des modèles probabilistes (di est une réalisation d'une variable aléatoire bien choisie) et on se donne comme objectif non pas que tout soit traité dans les temps, ce qui est trop exigeant (il faut avoir une grande valeur de C, donc un coût très élevé), mais que la condition "envoi en moins de 2 jours" soit satisfaite dans 99% des cas, par exemple. 99% des jours, ou 99% des clients, suivant l'exigence. Les plateformes de distribution gèrent cela bien mieux, car comme il y a de nombreux produits, les pointes sur un article sont gérées "dans la masse", et les fluctuations globales sont généralement minimes.

Quant au problème que tu sembles traiter (connaissant tous les d_i, choisir un C tel qu'on ait toujours satisfaction), je ne vois pas de méthode simple pour le traiter. Il se traite cependant facilement avec un tableur, une case variable pour C et une colonne de d_i. Si tu connais effectivement les d_i.

Cordialement.

(*) voir un cours de gestion de stocks.

[Médiat]

Bonjour,

Désolé, erreur !

[A voir en vidéo sur Futura]

[vanhoa]

Merci pour la reponse!

"tu ne maîtrises pas les valeurs di"
effectivement, c'est une inconnue et je veux exprimer ma capacite minimale necessaire en fonction des di

"si l'une d'entre elles est supérieure à 3C, l'envoi en moins de 2 jours ne sera pas possible, sauf embauche de personnel supplémentaire"
effectivement, et donc, je cherche a determiner mon C pour que ce soit toujours possible. C'est pour ca que je pense que la solution est dans ce que je disais:
pour respecter l'engagement il faut donc prendre la maximum de ces Qi, ainsi, l'engagement sera toujours respecte.

Je pense avoir trouve comment m'y prendre:
-chaque Q_i est un max de i termes
-ensuite il faudra faire le max de tous ces Q_i pour savoir le C
Donc cela signifie que je peux regrouper tous les termes de tous les Q_i sous un seul max, non?
J'aurais donc au final un max de (1+n)*n/2 termes (de Q₁ a Q_n) que je dois comparer a 3C
donc ensuite, est ce que je peux comparer chaque terme a 3C, en deduire le C pour chaque terme, et prendre le C maximum parmis les "(1+n)*n/2" C que j'aurais calcule?

par exemple:
Q₁ = d₁ <= 3C donc C >= Q₁/3
je continue pour les 2 termes de Q₂ qui sont: d₂+d₁-C et d₂
j'obtiens: C >= (d₂+d₁)/4 et C >= d₂
si j'avais seulement Q₁ et Q₂ je ferais le max entre les 3 C calcules, mais si j'ai jusque Q_n alors je continue...
Est ce que ca semble correct?

Merci

Vanhoa

[gg0]

Tu ne sembles pas avoir compris !

Tu veux un C supérieur à toutes tes quantités, mais tu ne les connais pas puisque tu ne connais pas les d_i. A quoi sert un calcul qui n'est pas utilisable ?

Ce que je te disais, c'est que quelle que soit la valeur C choisie, si tu as plus de 3C de commandes un jour, tu ne respecteras pas l'engagement. ta seule solution est de prendre C infini, ou au moins supérieur au tiers de toute quantité de commandes envisageable. Ce qui ne sert à rien !!

[minushabens]

Mais il a dit qu'il connaissait les di. Après on peut faire l'hypothèse (hasardeuse dans la vraie vie) que les di futurs resteront dans l'intervalle observé des di du passé, ou bien on peut utiliser les di observés pour estimer une distribution des di futurs mais ça suppose de faire un traitement probabiliste de la question, comme suggéré par gg0.

[gg0]

Gerard0 "tu ne maîtrises pas les valeurs di"
Vanhoa : "effectivement, c'est une inconnue et je veux exprimer ma capacite minimale necessaire en fonction des di"

Si c'est pour un cas concret (titre) et qu'on a une certaine expérience du passé, un traitement par tableur suffit pour trouver un C qui aurait convenu dans le passé et qu'on peut utiliser au caxs où "tout continuerait comme par le passé". Pas besoin de formule.

Cordialement.

[vanhoa]

Excusez moi, je pense que je me suis mal exprime.
Quand je dis que mes di je ne les connais pas, c'est parce que ce sont des variables pour moi, ce sont des projections du futur. Mais dans mon application, je dois les connaitre. Par exemple, je vais avoir tous les di quotidien de l'annee 2019. Je souhaite donc avoir une formule generale pour calculer mon C minimal qui me permet de respecter l'engagement. Si pour une certaine raison, les projections de 2019 changent, alors le C va automatiquement changer car je l'evalue avec une formule generale.
Le mieux est de montrer un exemple (image ci dessous). Je considere seulement 4 jours, donc de Q1 a Q4. J'ai utilise ma solution.
Pour 4 jours, c'est facile, mais si j'ai 2 annees de projections, c'est trop complique, je ne vois pas comment generaliser.

[gg0]

Ah OK !

Donc tu réduis ta règle à "si les demandes ne dépassent pas les prévisions, toutes les commandes seront fournies en 2 jours".
Et si tu regardes bien, tu as trouvé la méthode, puisque tu as choisi le max entre d₁/3,(d₁+d₂)/4,(d₁+d₂+d₃)/5, ... Il te suffit de généraliser :
.

Cordialement

[vanhoa]

Merci gg0!
Sauf erreur de ma par la formule de recouvre pas toutes les possibilites. En reprenant la formule, j'ai tente de l'adapter (c.f. image ci-dessous). Peut etre qu'il y a une facon plus simple. Merci a vous 2 pour avoir pris le temps de lire et repondre a mon probleme!

[gg0]

Effectivement,

je n'avais tenu compte que de la première colonne. par contre, ce n'est pas une somme double, mais un max sur double indice (un indice pour la colonne, un pour la ligne dans la colonne. On veut supérieur à (d1+d2)/4 et à d2/3, pas supérieur à (d1+d2)/4 + d2/3.

Cordialement.

[vanhoa]

Oui effectivement! Merci!
Bonne journee