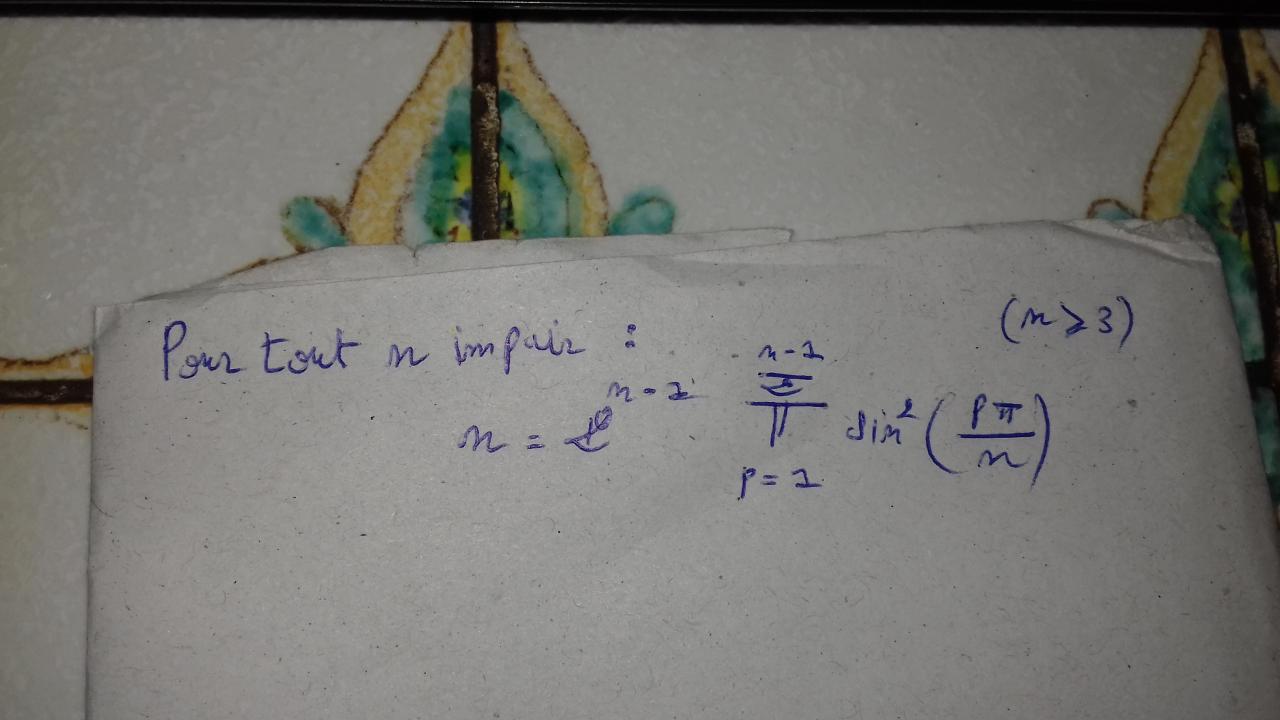Formule de tout nombre impair
Répondre à la discussion
Affichage des résultats 1 à 9 sur 9

Formule de tout nombre impair



  1. 14/02/2019, 21h10 #1
    invite43568a61

    Formule de tout nombre impair


    ------

    Salut
    Est ce que cette formule vrai?Nom : 20190214_220539.jpg Affichages : 110 Taille : 74,1 Ko

    -----
  2. 15/02/2019, 10h27 #2
    albanxiii
    Modérateur

    Re : Formule de tout nombre impair

    Bonjour et bienvenue sur le forum,

    Il faudrait commencer par définir les termes qui y apparaissent.
    Not only is it not right, it's not even wrong!
  3. 15/02/2019, 11h48 #3
    Médiat

    Re : Formule de tout nombre impair

    Bonjour,

    Pourquoi que les nombres impairs ?
    Je suis Charlie.
    J'affirme péremptoirement que toute affirmation péremptoire est fausse
  4. 15/02/2019, 11h55 #4
    Médiat

    Re : Formule de tout nombre impair

    D'ailleurs ont peut réécrire, pour tout entier
    Je suis Charlie.
    J'affirme péremptoirement que toute affirmation péremptoire est fausse
  5. Aujourd'hui
    A voir en vidéo sur Futura
  6. 15/02/2019, 11h59 #5
    Deedee81
    Modérateur

    Re : Formule de tout nombre impair

    Salut,

    Il y a une différence : il y a un carré dans la formule initiale.

    Question : on trouve facilement une démo de ça ?
    "Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
  7. 15/02/2019, 12h10 #6
    Médiat

    Re : Formule de tout nombre impair

    Citation Envoyé par Deedee81 Voir le message
    Il y a une différence : il y a un carré dans la formule initiale.
    J'ai remplacé le carré de la première moitié des indices par le produit de tous les indices (sin(k pi/n) = sin((n_k) pi/n))

    Citation Envoyé par Deedee81 Voir le message
    Question : on trouve facilement une démo de ça ?
    Pas cherché
    Je suis Charlie.
    J'affirme péremptoirement que toute affirmation péremptoire est fausse
  8. 15/02/2019, 12h58 #7
    invite6710ed20

    Re : Formule de tout nombre impair

    Bonjour
    Pour la démo, en utilisant les racines n_ième de l'unité on a l'identité
    Ensuite pour z=1, le module de chaque membre donne directement l'identité.
  9. 15/02/2019, 13h20 #8
    Deedee81
    Modérateur

    Re : Formule de tout nombre impair

    Citation Envoyé par Médiat Voir le message
    J'ai remplacé le carré de la première moitié des indices par le produit de tous les indices (sin(k pi/n) = sin((n_k) pi/n))[/COLOR]
    Ah oui, ça m'avait échappé. Merci,

    Citation Envoyé par JB2017 Voir le message
    Pour la démo, en utilisant les racines n_ième de l'unité on a l'identité
    Ensuite pour z=1, le module de chaque membre donne directement l'identité.
    Bien vu, génial. Merci.
    "Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
  10. 15/02/2019, 17h47 #9
    albanxiii
    Modérateur

    Re : Formule de tout nombre impair

    (j'ai lu dim au lieu de sin... d'où ma question !)
    Not only is it not right, it's not even wrong!
« Primitive d'une fonction racine particuliere | Cauchy Schwartz dans les Lp »

Discussions similaires

  1. Existe t-il un nombre parfait qui est impair?
    Par invite8dd52907 dans le forum Mathématiques du supérieur
    Réponses: 1
    Dernier message: 09/07/2016, 06h51
  2. nombre premier et nombre impair
    Par invite5a4fc698 dans le forum Mathématiques du supérieur
    Réponses: 11
    Dernier message: 08/01/2016, 17h49
  3. Logiciel R : nombre pair ? impair ?
    Par invite92876ef2 dans le forum Logiciel - Software - Open Source
    Réponses: 5
    Dernier message: 11/10/2012, 13h16
  4. Nombre impair et triangle rectangle
    Par invite9a322bed dans le forum Mathématiques du collège et du lycée
    Réponses: 10
    Dernier message: 25/07/2008, 17h07