Bonjour,
Dans le cadre de l'étude de la physique des plasmas, nous sommes amenés à étudier l'équation de Vlasov.
La 1ère photo définit certains termes.
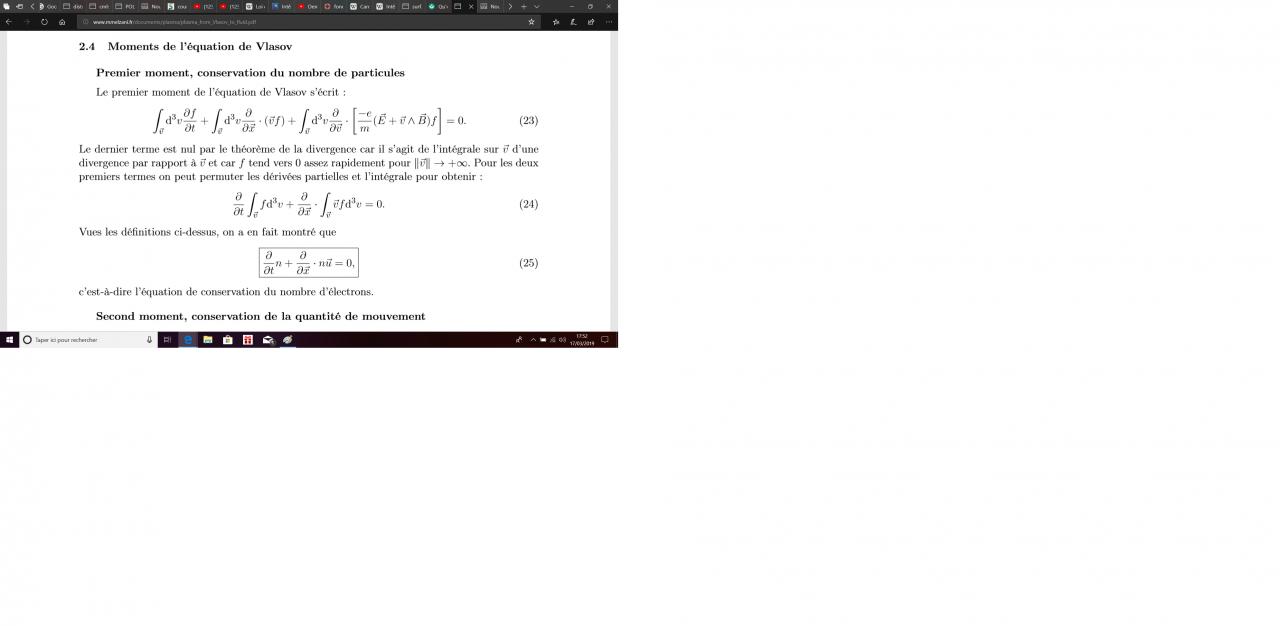
Sur la 2ème photo, je n'arrive pas a comprendre pourquoi l'intégrale avec le champs E est nul malgré les explications dessous.
Pouvez m'aider?
Sans titre.jpg
2ème photo:
def.jpg
Dernière modification par albanxiii ; 17/03/2019 à 20h13. Motif: typo titre
Les liens ne sont pas valides....
Très exactement, pas encore validés.
Ce qui ne dit pas qu'ils sont invalides.
Cordialement.
C'est exactement le même cas dans la ^photo ci-dessous pour la 3ème intégrale. Si quelqu'un pouvait un peu plus détaillé l'explication je serai bien content.
Les deux premières sont quasiment illisibles.
Je viens de voir, j'ai reposté une image dans mon 2ème message.
C'est le même problème et malgré a justification je peine à comprendre
A vue de nez, c'est plutôt un problème pour les physiciens (ne serait-ce que pour le contexte). Si tu n'as pas rapidement des réponses, demande à un administrateur de replacer cette discussion dans le bon forum.
Cordialement
Je crois cela releve bien des maths, concretement de la theorie des distributions. Je suis incompetent dans ce domaine,
Si corentinca se donnait la peine de taper sont problème avec LaTeX et des mots au lieu d'envoyer une mauvaise copié d'écran, on aurait dépassé le stade des suppositions.
Un petit effort !
Not only is it not right, it's not even wrong!
A sa decharge, ca doit etre tres chiant de mettre ces integrales en LaTeX... mais ca n'empeche pas de le faire bien sur.Envoyé par albanxiii
Ici F est un champ de vecteur.
Quand tu intègre la divergence de F sur un volume, genre intégrale de div F, c'est égal au flux de F sur la surface de ce volume. Le flux c'est l'intégrale de F sur la surface du volume.
Si le volume enfle jusqu'à l'infini, sa surface aussi, et si le champ F a la bonne idée de décroitre vers 0 PLUS VITE que la surface (qui croit en R²) alors la limite quand R tend vers l'infini du flux sera nulle.
Donc l'intégrale de la divergence aussi, à la limite.
NB : R est le "rayon" moyen du volume.
Le problème est que je ne comprend pas tes formules : est-ce que les égalités sont quand "v tend vers l'infini" ?
Je ne comprend pas non plus tes intégrales (pratiquement illisible) : tu intègre sur quoi exactement, un volume ?
Dernière modification par pilum2019 ; 17/03/2019 à 18h07.
Salut,
Je vais situer le contexte de l'équation.
Soit une population de particules chargées, de masse m et de charge q, décrite par la fonction de distribution en position et en vitesse F(r,v,t); cette fonction peut être interprété dans un cadre statistique comme le nombre moyen de particules dans un élément de volume drdv autour du points r,v.
On peut définir certaines variables hydrodynamiques, comme la densité : n(r,t) qui serait l'intégrale de cette fonction sur v (vitesse).
L'équation dans mon 2ème message, est une intégrale de l'équation de Vlasov sur la vitesse (et pas sur le volume) dans l'espace des phases.
Okaaaaayyyy!
D'accord, si j'ai bien compris, je dis bien si j'ai bien compris, mon explication précédente tient toujours;
J'avais parlé d'un champ de vecteur F(x,y,z) , et on calculait l'intégrale de la divergence de F(x,y,z) sur un volume d'espace en (x,y,z)
Avec ton explication ça revient au même : tu a un champ de vecteur F(continuons de l'appeler F pour simplifier), sauf que c'est F(vx,vy, vz), et si j'ai toujours bien compris, tu intègre sur TOUT l'espace, sauf que c'est un espace en (vx,vy,vz). En fait le noms changent mais la méthode est la même.
Ton document t'explique que tu intègre sur une boule d'espace de rayon R. En appliquant le théorème du flux (ou théo de la divergence), cela revient à une intégrale de surface (et non plus sur un volume).
Ton intégrale (la troisième donc) est égale à une intégrale sur une sphère de rayon R.
Attention : on est toujours avec les variables (vx,vy,vz). Ici, il s'agit d'une sphère de rayon R dans l'espace des vitesses. vx² + vy² + vz² = R².
Bon d'accord mais une intégrale de quoi, tu me diras ?
Ce flux, ou intégrale de surface c'est l'intégrale du produit scalaire du champ F avec le vecteur normal à la surface. Le vecteur normal ayant une intensité dS, ou dS est l'élément infinitésimal de surface associé au vecteur normal pris en un point donné de la surface.
Il n'est pas difficile de voir que ce flux est en valeur absolue inférieur ou égal à S fois max(F), où max( F) est l'intensité maximale du champ de vecteur F sur la surface.
La surface croit en R². Là, ton document suppose que max(F) décline vers 0 en moins que 1/R², genre 1/R^3. Donc le produit S fois max(F) va décroitre vers 0 quand R tend vers +oo.
Remarque: on fait tendre R vers +00 puisque c'est une intégrale sur tout l'espace en (vx,vy, vz), si j'ai bien compris.
Donc au final, ton flux est nul, et comme c'est égal à ta 3ème intégrale, tu as l'explication.
Dernière modification par pilum2019 ; 17/03/2019 à 20h03.
Merci beaucoup pour ces explications très claires.
Bonne soirée
