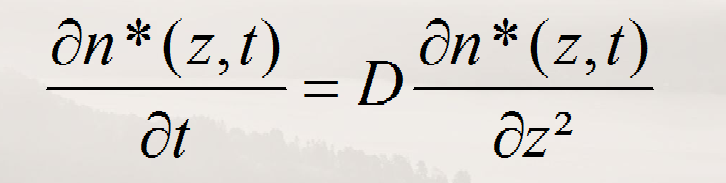Méthode des caractéristique
Discussions similaires
-
Par invite67c38467 dans le forum Physique
Réponses: 1
Dernier message: 04/09/2014, 16h37
-
Par invite3424471c dans le forum Mathématiques du supérieur
Réponses: 0
Dernier message: 07/01/2013, 22h02
-
Par invite4afd691f dans le forum Mathématiques du supérieur
Réponses: 0
Dernier message: 13/06/2012, 13h41
-
Par invite689a48fd dans le forum Géologie et Catastrophes naturelles
Réponses: 0
Dernier message: 06/01/2011, 14h12
-
Par invite60e37dfb dans le forum Mathématiques du supérieur
Réponses: 0
Dernier message: 27/12/2009, 17h52