Bonjour,
Besoin d'aide !
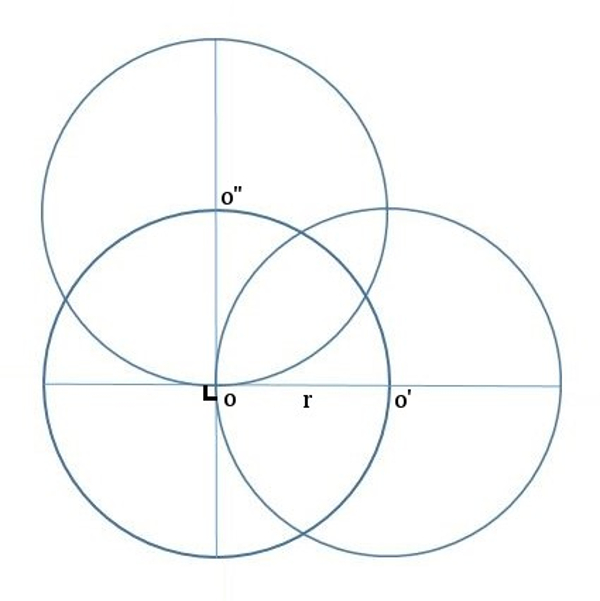
Soit trois disques de même rayon r disposés ainsi dans le plan :
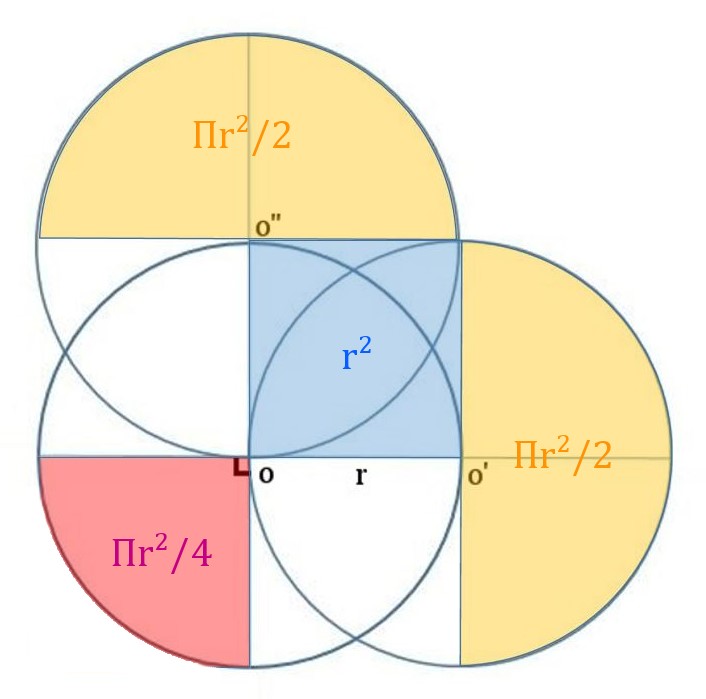
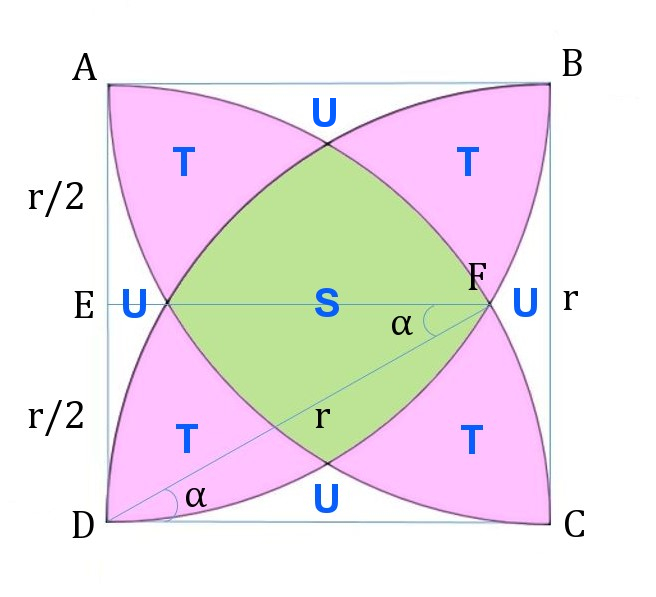
Quelle est la surface occupée par ces disques ?
Si chaque disque est le plan équatorial d'une sphère, quel volume correspond à ces trois boules imbriquées ?
Merci
Pour la surface des disques.
en appelant
A l'intersection "extérieure" ( à gauche ) des cercles O et O"
B celle ( tj "extérieure" ) des cercles O et O'
C celle des cercles O' et O"
la surface totale est la somme :
-de la surface du triangle "intérieur" ABC
-des trois morceaux de disques coupés par les droites AB ,AC, BC.
essai de croquis:
Pour ce qui est de la surface des 3 cercles, je pense avoir trouvé. Voici les aires les plus évidentes :
Pour les surfaces non colorées à déterminer, je les décompose comme suit :
Soit la droite EF a mi-hauteur du carré, U/2 vaut la différence entre le demi-carré et les surfaces du triangle EFD et de la portion de cercle FDC :
U/2=(r²/2)-[EF*(r/2)*1/2]-[Pi*r²*(alpha/360°)]
sin(alpha)=(r/2)/r=1/2 donc alpha=30°
EF=r*cos(alpha)=r*cos(30°)=(r* √3)/2
U/2=(r²/2)-[((r*√3)/2)*(r/2)*1/2]-[Pi*r²/12]
U=r²-[(r²*√3)/4]-[Pi*r²/6]
Et : r²-U=r²-r²+[(r²*√3)/4]+[Pi*r²/6]=r²*[((√3)/4)+(Pi/6)]
Ainsi l'aire totale A occupée par les 3 cercles est :
A = r²+2*(Pi*r²/2)+(Pi*r²/4)+2*[(r²*(√3)/4)+(r²*Pi/6)]
A=r²*[1+Pi+(Pi/4)+((√3)/2)+Pi/3]
A=r²*[1+((√3)/2)+(19*Pi/12)]
A≃6,84r²
Ça semble correct. Maintenant pour le volume des trois boules imbriquées, je ne sais pas comment m'y prendre !!!
Merci pour votre aide
bjr,
je ne vois pas bien comment tu passes de la première figure à la seconde.
mais qu'importe car je trouve le même résultat en partant de mon triangle + surfaces externes.
pour les sphères, je passerai bien par une intégrale en fct de la hauteur.
ce qui suppose de résoudre d'abord l'équation "générale" avec les même centres mais des r inf ( les cercles sont plus petits )
Cdt
