calcul d'une somme avec indice négatif parfois

[Salimkarim]

Salut
Comment faire si l’indice est k-i-1, k=1 et i=1, on obtient un indice négatif -1, dans le calcul des sommes pour les méthodes de transformations différentielles dans la résolution des équations différentielles.

Exemple:


-----

[minushabens]

bonjour, on ne sait pas ce qu'est r dans ta formule, ni ce qu'est W.

[gg0]

Bonjour Salimkarim.

A priori (*), la formule est mal écrite, r devant aller de 0 à k-1. Si ce n'est pas une erreur d'écriture, le contexte doit permettre de calculer W(-1,x). Et comme on ne sait pas d'où tu sors ça, difficile de t'aider vraiment.

A noter : rien n'interdit des indices négatifs dans une somme :


Cordialement.

(*) à cause du , et en supposant que W(0,x) est bien défini.

[Salimkarim]

Merci
C'est une relation de récurrence, r un indice variant de zéro à k. W une fonction de x et k.

[A voir en vidéo sur Futura]

[Salimkarim]

Bonsoir gg0
Merci
Justement W(-1,x); ne peut exister car k est un entier positif.!!!! effectivement W (0.x)=2lnx

[raymolk]

Justement W(-1,x); ne peut exister car k est un entier positif.!!!!

Mais il n'y a aucun lien entre ces deux choses : le fait que W(.,x) ne soit pas définie pour des entiers négatifs est totalement indépendant des valeurs de k.
Par ailleurs, dans ton premier message, tu dis « si l’indice est k-i-1 » : quel indice, et pourquoi introduire « i » ?
Tout ça n'a guère de sens…

[Salimkarim]

Bonsoir tout le monde
Pour éclaircir les choses la relation est tirée des propriétés de la méthode RDTM....VOIR PHOTO.

Le problème est que l'indice obtenu est parfois négatif comment faire???

[gg0]

Eh bien, dans la formule de ta photo, l'indice k-k₁-1 n'est jamais négatif. k₁ va de 0 à k-1, comme je le disais de ton r du premier message. l'indice obtenu n'est jamais strictement négatif. il varie de k-1 (k₁=0) à 0 (k₁=k-1).

[Salimkarim]

Ce que tu dis est exact, mais en appliquant une propriété de multiplications de ces transformées on obtient la formule voir photo. Et l'indice négatif est très fréquent dans ces problèmes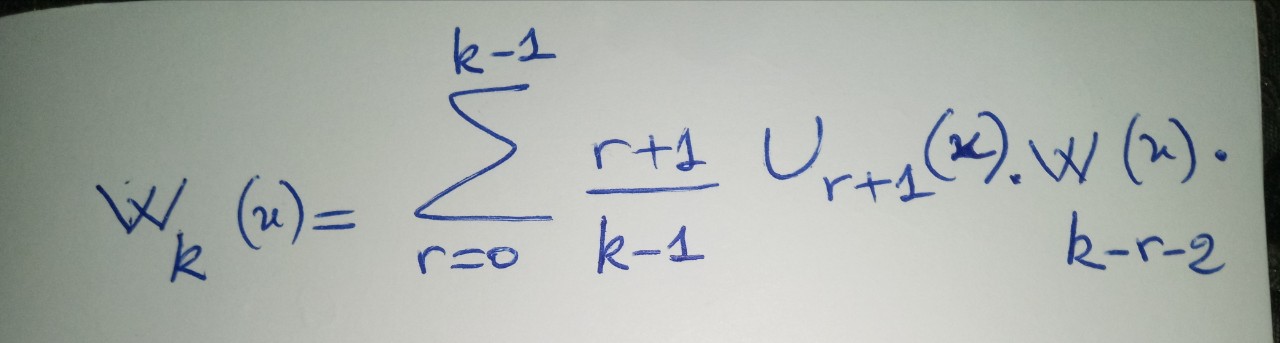

[ansset]

Oui, donc

On a : pour k=1 ; k1=0

et de même

etc..

[Salimkarim]

Merci...mais comment faire pour la formule de ma dernière photo?

[ansset]

Ce que tu dis est exact, mais en appliquant une propriété de multiplications de ces transformées on obtient la formule voir photo. Et l'indice négatif est très fréquent dans ces problèmes

possibilité:
l'application correcte de la propriété en question ( laquelle? ) n'aboutit pas à ce résultat
et de fait la somme doit s’arrêter pour r=k-2 dans le cas présent ( car je doute que W_-1(x) soit définie )

ps : ou bien implicitement , on n'en tient pas compte , mais je ne connais pas le contexte.

[ansset]

ou bien encore, la transformation abouti à un W_k-r-1(x) et non à un W_k-r-2(x)

[raymolk]

Ce que tu dis est exact, mais en appliquant une propriété de multiplications de ces transformées on obtient la formule voir photo. Et l'indice négatif est très fréquent dans ces problèmesPièce jointe 402849

Eh bien soit tu t'es trompé dans l'application de la formule, soit il existe un bout de définition quelque part que tu oublies, et qui donne sens à W_k pour k<0.

[gg0]

Une première formule écrite par Salimkarim, qui n'est pas la formule qu'il photographie, et maintenant une troisième formule qui sort de je ne sais où ! Ce n'est pas sérieux .. je laisse tomber, les gens qui changent la question quand on essaie de leur répondre m'insupportent.

[Salimkarim]

Je n'ai pas changé de problème, mais c'est le déroulement naturel des calculs, je peux demain photographier des formules avec le nouveau indice.
Merci beaucoup, pour tous ceux qui ont laissé une réponse, et j'apprécie beaucoup votre geste.

[ansset]

Je n'ai pas changé de problème, mais c'est le déroulement naturel des calculs, je peux demain photographier des formules avec le nouveau indice.
Merci beaucoup, pour tous ceux qui ont laissé une réponse, et j'apprécie beaucoup votre geste.

Sans le contexte de ces "transformations différentielles" et des règles applicables , il sera difficile d'apporter d'avantage de réponses.