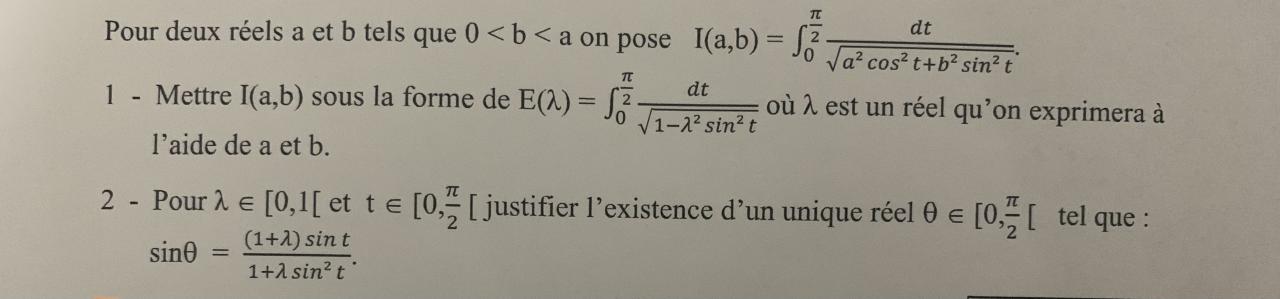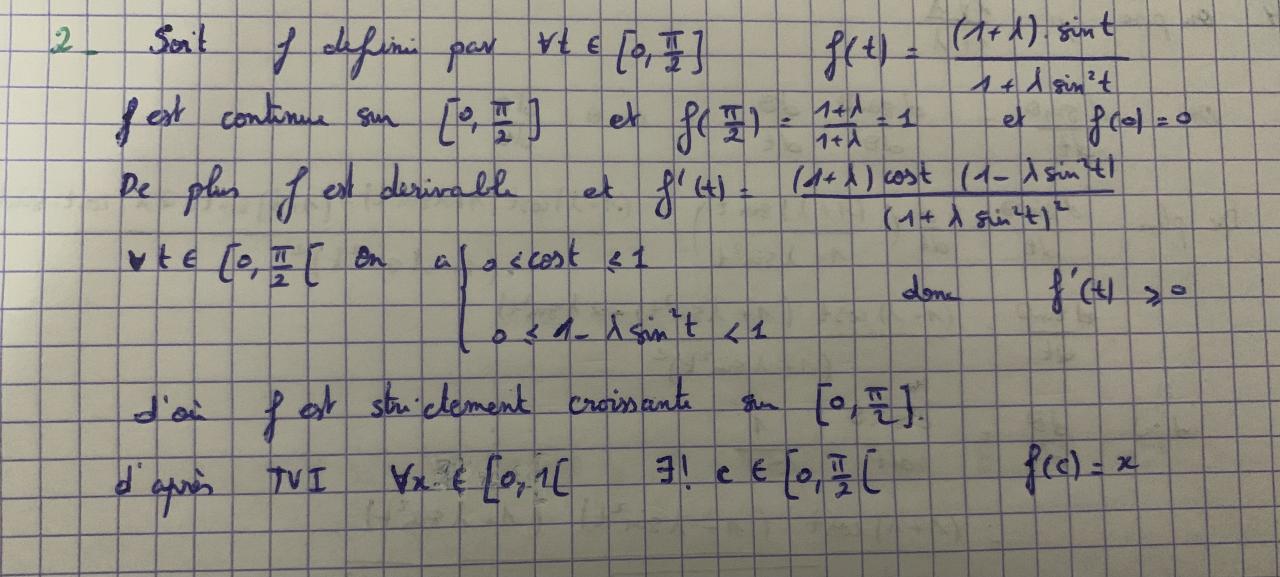Relation trigonométrique

[invitedc16fe1a]

bonjour
pouvez vous m'aider sur les deux questions suivantes sur lequelles je bloque
1/ecrire a^2*cos(t)^2+b^2*sin(t)^2 sous la forme 1-c^2*sin(t)^2 ou c s'exprime en fonction de a et b
2/pour c entre 0 et 1 , t entre 0 et pi/2 , mq il existe une unique x entre 0 et pi/2 tq sin(x) = (1+c)sin(t)/ (1+c*sin(t)^2)

pour le 1 j'ai essayer ecrire 1-sin^2 = cos^2 mais je garde toujours le a^2 , j'ai aussi essaye de factoriser avec a^2 mais sans resultat
pour le 2 j'ai essayer d'encadrer mais j'obtiens que l'expression est entre 0 et 2 ce qui ne me permet pas de conclure
merci
-----

[jacknicklaus]

Bonjour,

si l'exercice est d'écrire a²cos²(t) + b²sin²(t) sous forme 1 - c²sin²(t), il est clair qu'il y a erreur d'énoncé.
On le voit avec t = 0. La 1ère forme donne a², la seconde donne 1. il y a comme un problème.

[invitedc16fe1a]

Voici l’énoncé exacte j’ai peut hormis quelques choses en déformant un peu

[jacknicklaus]

Donc erreur d'énoncé. Je te suggère soit d’abandonner l'exercice en signalant le problème à ton prof, soit, beaucoup mieux, de proposer de continuer en écrivant l'expression sous le radical comme suit :

a²(1 - c²sin²(t)).

ne pas oublier d'utiliser a > b > 0

[A voir en vidéo sur Futura]

[invitedc16fe1a]

Bonjour
Dans ce cas là l’erreur d’énoncée a t elle un impact sur la question suivante?
Merci

[jacknicklaus]

à première vue, non.

[invitedc16fe1a]

Bonjour
Pour la question 2 l’encadrement est il la piste à creuser , ou bien théorème d’existence comme le TVI ou le th de la bijection serait plus concluant?
Merci

[jacknicklaus]

qu'as tu essayé ?

[invitedc16fe1a]

J’ai essayer l’encadrement ça me donne un intervalle plus large que nécessaire [0,2]
Puis j’ai essayer le TVI sur la fonction f(t)=“l’expression à gauche du sinus”
Je trouve f(pi/2)=1 et f(0)=0
Elle est continue et dérivable , sa dérivée par rapport à t est positif, donc strictement croissante j’obtiens l’existence et l’unicité de thêta mais c’est bel et bien le sin dans l’expression qui me pose problème , je ne vois pas comment le faire apparaître

[jacknicklaus]

Pourtant, tu as fini cet exercice.
Tu as démontré que tout réel x entre [0,1[ avait un antécédent unique t, tel que f(t) = x. Avec t dans [0,pi/2]
Or quelle est l'image de sin(z) avec z dans [0,pi/2] ? Sur cette intervalle, la fonction sinus est elle bijective ? Conclusion ?

[invitedc16fe1a]

Bonjour
En effet f(t) et sin sont toutes les deux bijectives de [0,pi/2[ vers [0,1[ , mais qu’est ce qui me permet de dire qu’elles sont égales?

[jacknicklaus]

f(t) = sin(t) n'est pas ce qui est demandé. relis bien la question posée.

[invitedc16fe1a]

Voici où j’en suis , serais ce correct de dire
Prenons x=sin(theta) ?

[azizovsky]

Voici l’énoncé exacte j’ai peut hormis quelques choses en déformant un peuPièce jointe 428335

donc :

avec

[invitedc16fe1a]

Justement à propos de la formulation de la question je me demande est ce que “écrire I(a,b) sous la forme E(lambda)” signifie I(a,b)=E(lambda)?

[azizovsky]

Non sauf si a=1.

[jacknicklaus]

Voici où j’en suis , serais ce correct de dire
Prenons x=sin(theta) ?

C'est theta qu'on cherche. Vu ce que tu as montré, il te suffit de dire que theta = Arcsin(f(t)) convient (car bien défini pour tout t et lambda).