Trigonométrie et coordonnées cylindriques

[Val3riane]

Bonjour,
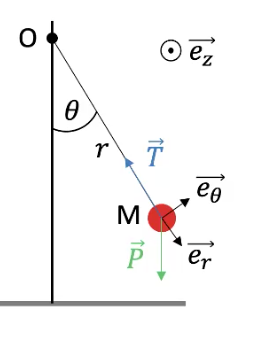
Dans mon cours, on désigne le mouvement d'un pendule caractérisé par un point M, et on part d'une principe que seul le poids est une contribution aux forces
On note alors : P = mg cos θe_r - mg sin θ e_θ

Mais je ne comprends pas deux choses !
1) Comment peut on savoir que P va être définit (en partie) par cos θe_r et sin θ e_θ ? Je ne comprends pas pourquoi ce "cos" et ce "sin" ici et pas par exemple sin θe_r et cos θ e_θ ? Et d'ailleurs, généralement je n'arrive pas à comprendre ce qui nous permet de dire que l'on va utiliser pour tel vecteur cos, puis pour l'autre sin...

2) Ensuite, pourquoi faire mg cos θe_r - mg sin θ e_θ ? C'est le "moins" que je n'arrive pas du tout à visualiser

Est-ce que quelqu'un pourrait m'aider svp ?

Merci beaucoup
-----

[Rhopi]

Bonjour,

il suffit de projeter sur les 2 axes choisis et ensuite de tenir compte du sens des projections par rapport aux axes.

Sans ta figure je pense qu'on ne peut pas en dire plus

[Val3riane]

Voici la photo de mon exercice

Effectivement mon prof parlait de "projections" mais je j'arrive pas à la visualiser dans ce cas-là

[gg0]

Bonjour.

Il s'agit simplement de la décomposition d'un vecteur dans une base. Qui s'appuie sur la propriété de projection des vecteurs :
Si u et v sont des vecteurs, u étant de norme 1, le projeté de v sur u (la composante de v dans la direction u) est cos(u,v).u.
L'angle entre e_r et P est θ, d'où le mg cos θ . e_r.
L'angle entre e_θ et P est θ+pi/2, d'où le - mg sin θ . e_θ (cos(θ+pi/2) = - sin θ).

Cordialement.

NB : Ton prof connaît parfaitement ce qu'on faisait en trigonométrie dans les classes de première (S et STI). Ça pourrait te servir de reprendre un livre de première STI des années 90.

[A voir en vidéo sur Futura]

[Val3riane]

Super merci beaucoup !
Et merci également pour l'information !