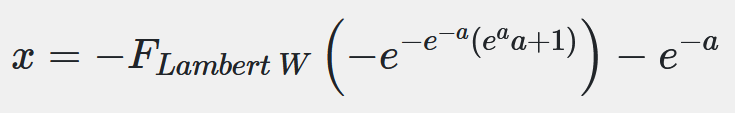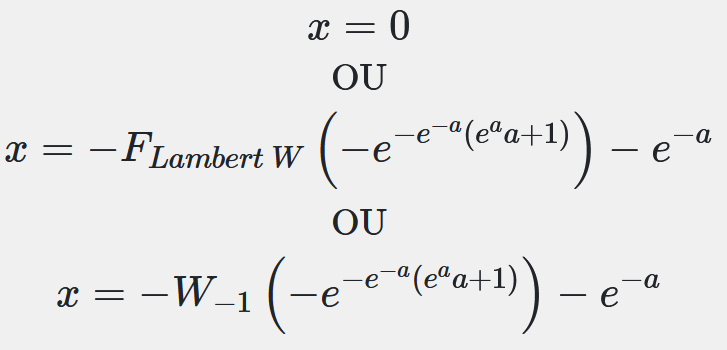Bonjour à tous,
je vous écris car je ne parviens pas à mes fins.
Je m'explique.
Voila le contexte de mon problème :
Je me suis fait une feuille de calcul qui me génère une courbe de forme exponentielle.
Cette courbe est destiné à corriger une courbe linéaire.
La feuille de calcul me donne directement les valeurs du nombre voulu d'éléments (d'un tableau) à copier coller dans mes programmes (langage C, micro-contrôleur).
Pour information toute la feuille de calcul fonctionne parfaitement.
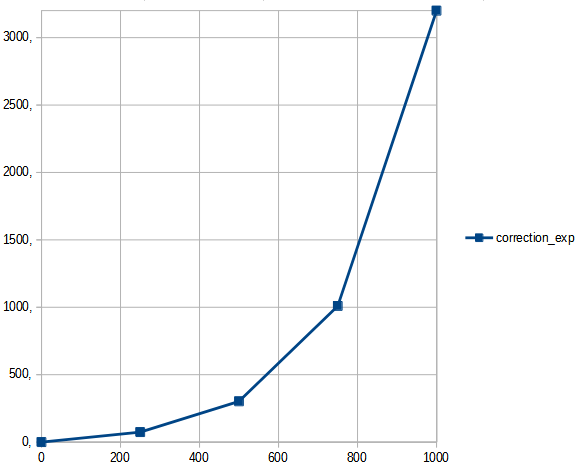
Voici un exemple de courbe calculé avec 5 points :
Mon niveau mathématique n'étant pas foufou, j'utilise régulièrement les solveurs mathématique, lorsque cela devient nécessaire.
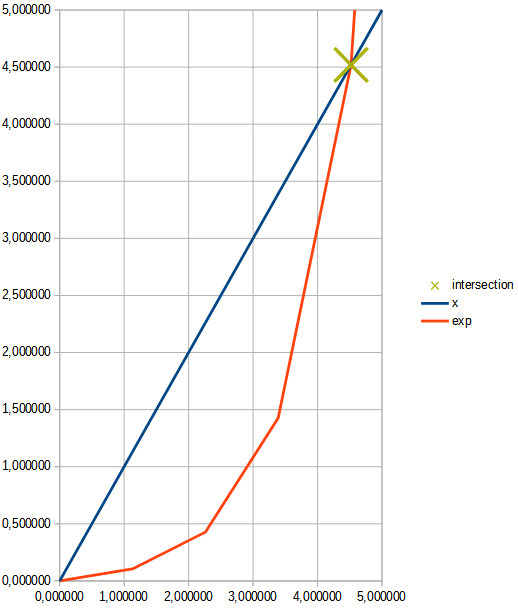
J'ai deux courbes, et il me faut le point d'intersection.
courbe 1 : f(x)=x
courbe 2 : f(x)=(e(x-a))-(e(-a))
Il me faut donc résoudre :
x=(e(x-a))-(e(-a))
Je veux calculer "x"
"a" est une constante contenu dans une cellule. C'est un paramètre que je peux régler.
Le solveur de ma calculatrice (TI-83 premium) fonctionne direct, je lui donne "a" et il me donne "x", OK très bien.
Maintenant il me faut l'intégrer dans ma feuille de calcul.
Pour l'instant la valeur est fixe et calculé à l'aide de la calculatrice
Le solveur sur internet que j'utilise me donne la formule suivante :
Pour résoudre le problème il faut utiliser la fonction de Lambert W (Oméga), qui est une fonction qui fait intervenir les nombres complexe.
Voila une fonction mathématique que je ne connaissais pas.
J'ai fini par trouver une macro pour libre office, qu'il m'a fallu modifier pour qu'elle fonctionne.
Voir le sujet que j'ai déja posé (le début du sujet est le même) :
https://forums.futura-sciences.com/l...-lambertw.html
Donc la macro m'a l'air de fonctionner correctement.
Par contre je ne parviens pas à obtenir le bon résultat.
Je pense que je ne l'utilise pas convenablement.
Dans tout les cas je ne comprend pas très bien les différentes notations.
je m'explique :
Le solveur me donne en réalité 3 solutions :
Si je dis au solveur de me faire une application numérique avec une valeur à la place de "a", il me donne la bonne valeur.
x=0 ne m'intéresse pas.
Les deux courbes se coupent aussi en zéro, mais ça n'a aucun intérêt pour moi.
Par contre sur les deux autres solution, il y en a une qui me donnera la bonne solution.
Concrètement je ne sais pas quelle est la différence entre la fonction de Lambert et la fonction de Lambert-1
La macro me propose deux fonctions :
LAMBERTWc(a, b) => "a" partie réelle et "b" partie imaginaire
LAMBERTW(a) => "a" partie réelle, puis fait appel à LAMBERTWc(a, b) avec "b" fixé à 0
Je me suis dis :
La fonction LambetW est pour W=0 donc un imaginaire =0
La fonction LambertW-1 est pour W=-1 donc un imaginaire =-1
Après de multiples essais, je ne parvient pas au bon résultat, je fait donc fausse route.
Pour info, avec a=3, x doit valoir 4,5193171784287
Je pense qu'il me faut, soit donner à la fonction un calcul un peut différant (inverse, opposé...), soit la modifier pour que la condition initiale soit différente, ou autre.
Le niveau mathématique me dépasse complètement, d'où ma demande d'aide.
Si quelqu'un à déjà utilisé la fonction de LambertW et qu'il voit le problème, qu'il ne se prive pas de m’expliquer que j'ai rien compris, car en effet ça m'a bien l'air d’être le cas.
Aussi, si il y à moyen d'arriver à un résultat sans utiliser LambertW, ça m’intéresse aussi.
Voici les solveurs internet que j'ai utilisé :
dcode : https://www.dcode.fr/solveur-equation
symbolab : https://www.symbolab.com/solver
symbolab me donne une formule différente, mais j'imagine que les deux sont équivalentes.
Voici le lien vers le code de la macro :
https://gist.github.com/m93a/a0199c4...6810daa46dd92d
-----