Accéléromètre XYZ sur axe tournant.

[maho]

Bonjour,

Je sèche sur un problème depuis un moment.
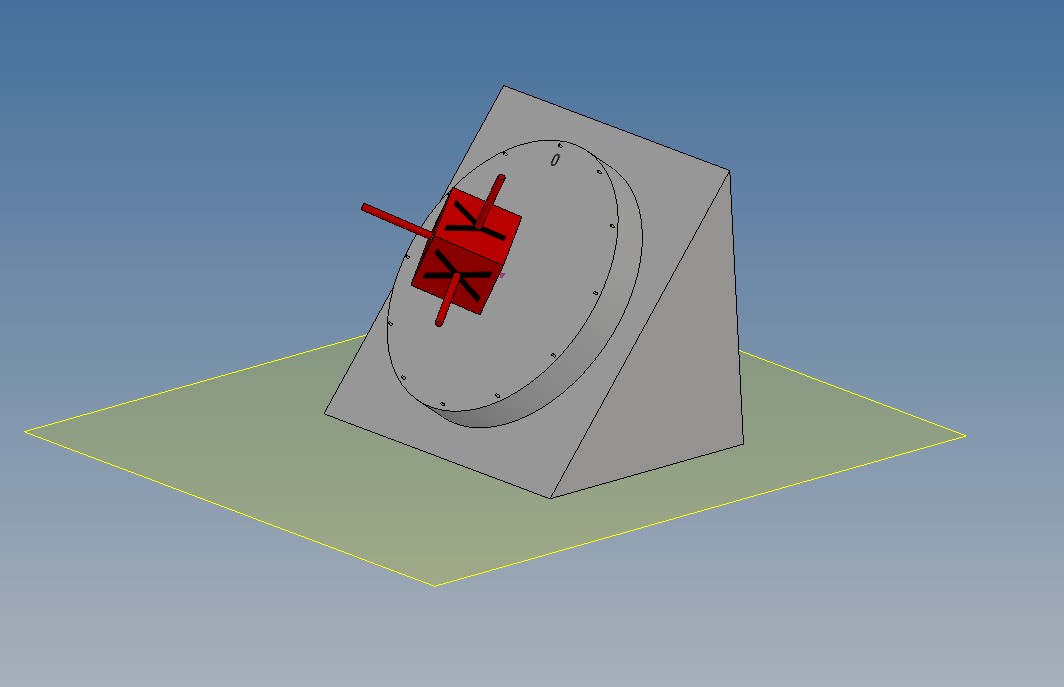
On a un axe qui fait un certain angle avec l'horizontal. >0° à <=90°
Sur cet axe tournant, on a un accéléromètre qui est fixé, mais dans un sens quelconque.

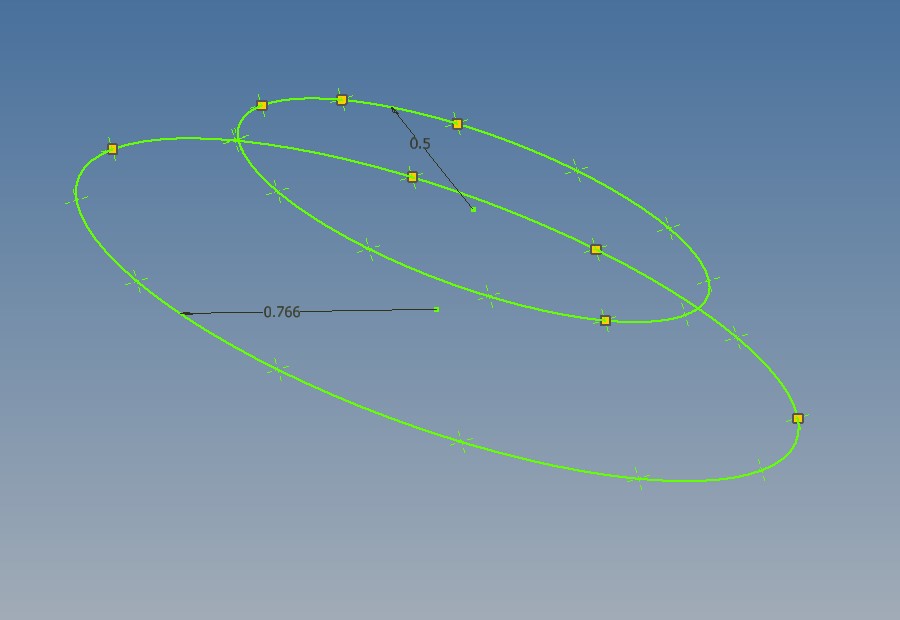
Est ce qu'il est possible de déterminer l'angle de cet axe avec l'horizontal et relevant quelques points XYZ de l'accéléromètre, en tournant l'axe.
Et par la même occasion, connaitre l'angle de rotation de l'axe entre chaque points.
J'imagine qu'il faudra minimum 3 points.

Est ce qu'il y a quelqu'un de calé en Géométrie analytique? Merci d'avance.
-----

[gg0]

Bonjour.

Ta question est loin d'être claire. Veux-tu utiliser des mesures d'accélération données par l'accéléromètre quand tu fais tourner ton axe en gardant le même angle avec l'horizontale (1) ? Ou utiliser des points situés sur l'accéléromètre (qui pourrait être n'importe quel objet) pour déterminer la direction de l'axe (2) ?
Dans le cas 1, si ton axe est fixé en un point d'un plan horizontal, tu pourras au mieux définir (de façon peu précise) le cercle que parcourt ton accéléromètre sans connaître sa position (seulement son rayon), puisque tu n'as pas de référence. A moins que tu aies d'autres données cachées.
Dans le cas (2), il faut savoir ce qui se passe.

Un schéma de principe serait utile.

Cordialement.

[maho]

En fait le plan incliné est fixe par rapport à l'horizontal.
le capteur XYZ est solidaire et fixe par rapport à l'axe tournant.

Les mesures d'accélération se ferait lorsque l'axe ne bouge pas pour éviter une accélération inertielle.
Et je voudrais avec quelques mesures en tournant l'axe déterminer l'angle du plan incliné (Environ 50° dans cette exemple)
Donc le vecteur XYZ du capteur serait toujours dirigé contre le bas.
J'ai essayé en calculant les angles des vecteurs normales (perpendiculaire) à 2 points, mais je n'y arrive pas..

Par exemple pour un plan à 50° et en faisant une mesure en tournant l'axe tous les 30° j'obtiens ça:

Axe X Y Z
0 0.84 -0.10 0.53
30 0.58 -0.29 0.76
60 0.22 -0.31 0.93
90 -0.14 -0.15 0.98
120 -0.41 0.13 0.90
150 -0.51 0.47 0.72
180 -0.41 0.77 0.48
210 -0.15 0.96 0.25
240 0.21 0.97 0.09
270 0.57 0.82 0.03
300 0.84 0.54 0.11
330 0.94 0.20 0.29



J'ai dessiné un schémas de principe.

[maho]

En fait, je viens de trouver par hasard, et j'explique çi-dessous pour les interessés!

Le nuage de point passe par un cercle parfait, et l'angle du plan incliné est l'arcsinus du rayon de ce cercle.

Plan à 50° = asin(0.766)
Plan à 30° = asin(0.5)

Donc avec 3 points on peut déterminer l'angle du plan.
Maintenant le problème, c'est de trouver analytiquement le rayon du cercle qui passe par ces 3 points dans l'espace! Mais je pense y arriver...

[A voir en vidéo sur Futura]

[gg0]

Ah, tu as changé de problème. Et tu sembles utiliser un accéléromètre comme outil pour te donner des positions absolues (ce qu'il ne fait pas spontanément).
Supposons que tu aies les positions absolues de différents points. Avec trois points, tu définis le plan dans lequel tourne ton accéléromètre. Comme tu peux le faire tourner de 180°, tu as deux points diamétralement opposés, ce qui te donne le diamètre du cercle (je n'ai pas compris ton histoire d'arcsinus, le rayon du cercle dépendant de par rapport à quoi on fait tourner, si la mesure est faite sur l'axe de rotation le rayon est toujours nul).
Une dernière chose : Les erreurs de mesure peuvent rendre les calculs totalement faux.

Cordialement.

[mach3]

La norme de la mesure avec l'accéléromètre sera toujours d'à peu près 1 s'il reste en mouvement rectiligne uniforme par rapport au sol (et en particulier s'il est immobile par rapport au sol). Ainsi, si on représente dans un repère qui porte les composantes de l'accélération suivant les axes x, y et z propre à l'accéléromètre toutes les mesures dans toutes les orientation possible de l'accéléromètre, on obtient une sphère. Si on restreint à certaines orientations, par exemple celle obtenues quand on autorise la rotation autour d'un axe seulement, les mesures vont être sur un cercle de cette sphère. En effet si l'orientation de l'accéléromètre tourne autour d'un axe alors dans le repère d'accéléromètre, le vecteur accélération tourne lui-aussi autour d'un axe et décrit donc un cône, dont la base est un cercle sur la sphère. Des caractéristiques de ce cercle, on doit pouvoir extraire des informations sur l'axe autour duquel l'accéléromètre tourne, mais ça va nécessiter du temps pour le démontrer... En tout cas intuitivement, si l'axe de rotation est colinéaire à l'accélération de la pesanteur, on aura un cercle de rayon nul et si l'axe de rotation est orthogonal à l'accélération de la pesanteur, on aura un grand cercle de la sphère (un équateur).

Peut-être qu'une démarche expérimentale comme celle déjà entamée amènera à des résultats concret plus rapidement qu'une démonstration mathématique.

m@ch3

[gg0]

Manifestement, il me manque des connaissances sur les accéléromètres (*), qui ne relèvent pas des mathématiques. J'en déduis que la question est posée au mauvais endroit, qu'il ne s'agit plus vraiment d'un problème mathématique. S'il t'arrive d'avoir un problème mathématique, Maho, prière de le dégager complétement de son substrat physique pour qu'il relève du forum.

Cordialement.

(*) A priori, un accéléromètre mesure des accélérations; quand il est fixe, il n'y a plus d'accélération. la mesure directe est nulle. Ce que vous appellez ici un "accéléromètre" est un objet qui fait autre chose, et sans le connaître, on ne peut pas deviner.

[mach3]

(*) A priori, un accéléromètre mesure des accélérations; quand il est fixe, il n'y a plus d'accélération. la mesure directe est nulle. Ce que vous appellez ici un "accéléromètre" est un objet qui fait autre chose, et sans le connaître, on ne peut pas deviner.

De base un accéléromètre mesure l'accélération propre, donc posé au sol, il donne une accélération égale et opposée au champ de pesanteur (donc 9.8m/s² vers le haut) et il mesure 0 en chute libre. Il faut "tricher" pour avoir l'accélération par rapport au sol (il me semble qu'on le couple à un gyroscope pour pouvoir retrancher l'influence de la pesanteur toujours dans la bonne direction). Mais bon, on ne va pas développer plus, ce n'est pas la bonne section.

m@ch3

[mach3]

Manifestement, il me manque des connaissances sur les accéléromètres (*), qui ne relèvent pas des mathématiques. J'en déduis que la question est posée au mauvais endroit, qu'il ne s'agit plus vraiment d'un problème mathématique. S'il t'arrive d'avoir un problème mathématique, Maho, prière de le dégager complétement de son substrat physique pour qu'il relève du forum.

De ce que je comprends, mathématiquement, on a vecteur de norme 1 suivant l'axe z d'un premier repère (celui du sol) et on cherche quelles sont les coordonnées de ce vecteur dans un second repère (celui propre à l'accéléromètre) qui est tourné arbitrairement par rapport au premier et on cherche à voir comment les coordonnées de ce vecteur évoluent dans ce second repère si on le fait tourner le second autour d'un axe. Ou inversement, à partir des coordonnées du vecteur dans différentes positions du second repère par rapport au premier, on cherche à savoir suivant quel axe on a fait tourner ce second repère.
Maho pourra préciser.

m@ch3

[gg0]

Merci pour les informations.

Cordialement.