Volume calotte sphérique

[invite118c6414]

Bonjour à tous et merci de votre attention.

Dans le cadre de mon cours de métallurgie, j'aimerais savoir le raisonnement menant à la triple intégrale pour une calotte sphérique (j'ai le résultat, mais je n'arrive pas à trouver les bornes pour mon intégration).

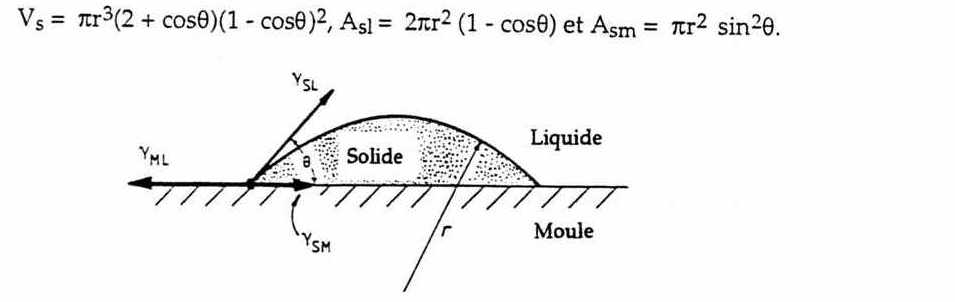
Comme donnée, j'ai l'angle a délimitant la calotte supérieure (c'est-à-dire l'angle entre le plan coupant la sphère à une certaine distance de l'origine et une droite tangente à la sphère à un point d'intersection avec le plan).

Merci beaucoup de vos pistes!

Follium
-----

[invite6b1e2c2e]

Salut,

Tu devrais nous en dire un peu plus. Qu'est ce que cette intégrale est censée représenter ?

__
rvz

[invite118c6414]

Ah oui oups, désolé.

C'est pour obtenir le volume (et la surface, mais bon ca, ca ne sera pas trop difficile une fois que je verrai un peu plus clair sur le volume)

Merci beaucoup de ton attention!

Follium

[invite6b1e2c2e]

Ok. Bon, en fait, je viens de m'apercevoir que c'était écrit dans le titre, alors j'aurais du m'en douter.

Donc, si je comprends bien ta question, tu te demandes pourquoi une intégrale triple représente effectivement un volume, c'est bien ça ?

__
rvz

[A voir en vidéo sur Futura]

[mécano41]

Bonjour,

Avec les données jointes, l'intégrale est celle-ci :



Elle donne :



Bon courage

[mécano41]

J'ai oublié : h c'est la distance AB

[invite118c6414]

En fait il y a un autre paramètre à prendre en compte en fait, mais je n'arrive pas à le relier à un paramètre de ta formule, je joins la figure avec le paramètre théta

Merci beaucoup!

Follium

[mécano41]

Bonjour,

D'après ton premier post, ton angle "a" est l'angle de la tangente à la base de la calotte. C'est donc l'angle theta de ton dernier post. Sur mon croquis c'est l'angle DOE. Attention à ne pas faire de confusion avec "mon" theta!

Dans mon calcul, (R-h)=AO=R.cos(theta)

Enfin... c'est ce que j'ai compris.

A bientôt

[Bruno0693]

Bonjour,

Avec les données jointes, l'intégrale est celle-ci :



Elle donne :



Bon courage

Bonjour,

Je m'intéresse également à la question du calcul d'une calotte sphérique.

Si je comprends bien, tu as utilisé les coordonnées cylindriques ?

Il y a une chose qui me paraît bizarre dans tes intégrales, tu écris :



Je ne comprends pas comment z peut figurer dans la borne d'intégration ?

En fait il faudrait lire



non ?

Mais je ne retrouve pas le même résultat que toi, je trouve

Qu'en penses-tu ?

[invite5580468a]

Salut, une réponse qui pourrait toujours servir,

L'intégrale générale s'écrit :



L'intégration donne :



Et enfin l'intégration de cette intégrale amène au résultat :



Ce qui peut être intéressant ce serait de chercher ce même résultat mais en utilisant les éléments d'intégration sphérique qui a une idée ????

Saluti !!!

[invite9e790ccf]

Bonjour, ça va?.

Je trouve très intéressant cette discussion, en effet, j´ai un problème pareil, mais je voudrais calculer le volume de la calotte sphérique mais j´ai touts les données pour utiliser la formule V = πh2(3r − h)/3, sauf le rayon de la circonférence.

Vous sauriez comme est que je peu faire?.

Merci d´avance.

Xer