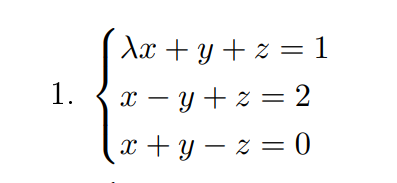triangulation de Gauss

[ICILabas]

Bonjour,

donc voilà j'ai un exercice de système d'équation qui me parait simple, mais je bloque tout de fois dessu.



Le voici, concernant la démarche utilisé pour mes tentatives de résolutions j'essaie de mettre la triangulation de Gauss en pratique mais rien ne fais je bloque.
De plus, je ne comprend pas trop comment le résoudre puisqu'on me donne uniquqement 3 expressions alors que j'ai 4 inconnus.

Si cela peut vous aidez voici l'énoncé en entier : Résolvez et discutez selon les valeurs de λ ∈ R les solutions des systèmes
d'équations suivants.

J'ai essayé de supprimer le lambda dans mes calcules, mais cela ne m'aide pas et en y réflichisant cela ne fait changer que le système d'équation.
Je me suis dit que peut-être cela a-t-il avoir avec les valeurs porpres, mais je ne suis pas trop sûr.

Merci pour l'aide que vous allez apporter
-----

[gg0]

Bonjour.

"selon les valeurs de λ ∈ R" permet de comprendre que les inconnues sont les trois autres lettres. Donc tu as bien trois inconnues, x, y et z. λ est comme un 2 ou un -3, sauf que tu ne connais pas la valeur et qu'il va falloir envisager tous les cas.
Donc tu appliques la triangulation de Gauss, et, pour ne pas être gêné par λ, tu traiteras la lettre x en dernier.

Bon travail !

[MissJenny]

Dans cet exercice tu dois raisonner comme si tu avais seulement 3 inconnues x,y,z et faire comme si lambda était fixé. Pour chaque valeur de lambda (peut-être pas toutes, à vérifier...) tu as une solution (x,y,z) donc en fait tu as une courbe de R^3 paramétrée par lambda.

[ICILabas]

Merci pour vos 2 réponses, j'y vois maintenant un peu plus clair, mais lorsque que vous dites que toutes les solutions de lambda ne sont pas possibles. Cela veut-il dire que je doit chercher un domaine ? ou alors pour poser ma question d'une autre manière comment puis-je écrire toutes les solutions possible de lambda.

Car, ici j'ai trouvé comme réponse : x=1 ; y=lambda/2 ; z = (2+lambda)/2
mais lorsque j'essaie de remplacer lambda par 0, mes système d'équation sont correcte mais si je le remplace par tous autres nombres réels positifs ou négatifs, la première expression devient fausse.

[A voir en vidéo sur Futura]

[gg0]

Je le répète : λ n'est pas une des inconnues. C'est ce qu'on appelle un paramètre.
Quand tu écris "toutes les solutions de lambda ne sont pas possibles" tu montres que tu n'acceptes pas le rôle que joue λ ici : Celui d'une lettre qui n'est pas une inconnue.
Il faut que tu fasses aussi attention à ce qu'on t'écrit : "lorsque [que] vous dites que toutes les solutions de lambda ne sont pas possibles." ?? je n'ai jamais dit ça !!

Je ne comprends pas ce que tu racontes à la fin. Qu'est-ce qui devient faux quand tu "le remplace(s) par tous autres nombres réels positifs ou négatifs"

[Gwinver]

Bonsoir.

Qu'est-ce qui devient faux quand tu "le remplace(s) par tous autres nombres réels positifs ou négatifs"

Je crois qu'il veut dire qu'au moins l'une des équations n'est pas vérifiée lorsque Lambda est remplacé par une autre valeur que zéro.

Par exemple, pour Lambda = 1
avec : x=1 ; y=lambda/2 ; z = (2+lambda)/2
la première équation devient : x + y + z = 1 soit : 1 + 1/2 + 3/2 = 1 qui est faux.

Il faut d'abord vérifier les valeurs trouvées en fonction de Lambda.
Ensuite, l'énoncé demande explicitement de vérifier s'il existe une classe de valeur pour lesquelles le système d'équation est bon.

[jacknicklaus]

Car, ici j'ai trouvé comme réponse : x=1 ; y=lambda/2 ; z = (2+lambda)/2

Ce résultat est faux, sauf pour x = 1 qui est correct et qui s'obtient immédiatement en additionnant les équations 2 et 3.

[gg0]

Moi j'attends une réponse de ICIlabas, et le mieux serait qu'il expose comment il a trouvé ça.

[ICILabas]

Bonjour, je pense m'être mal exprimé, mais quand je disais que si je remplace lambda par un nombre réels qui est autre que zéro ; comme la comprit Gwinver la première expression devient fausse.

Concernant, le procédé de mes calcules voici la feuille :

[gg0]

ICILabas,

tu n'as pas trouvé "x=1 ; y=lambda/2 ; z = (2+lambda)/2 ", mais x=1 ; y= - lambda/2 ; z = (2-lambda)/2 (regarde ce que tu viens d'envoyer).
Et pour toute valeur de lambda, le système est bien vérifié. Par exemple, pour lambda= 5, le système est
5x+y+z=1
x-y +z=2
x -y -z =0
qui a bien comme solution x=1,y=-5/2, z=-3/2

Cordialement.

NB : Pour lambda=0, ta fausse solution donne exactement la bonne ! Puisque -lambda = lambda dans ce cas.