Bonjour,
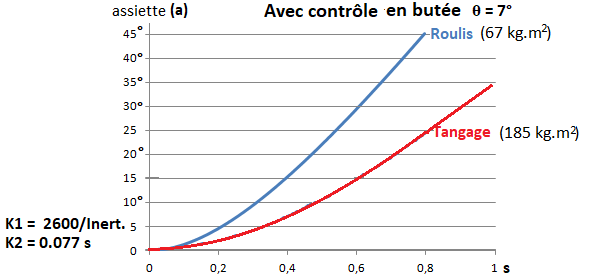
Pour une application physique personnelle, j'aimerais résoudre cette équation différentielle: : K1 Sin(θ – K2. a') - a" = 0
dans laquelle θ est un angle constant <10° , K1 et K2 sont des constantes, a(t)) est un angle dépendant du temps.
Merci de m'accorder un peu de votre temps .
Bonjour.
Un logiciel de calcul formel donne une équation en a', utilisant des arcsin et les fonctions spéciales cos intégral et sin intégral (aa=a') :
Ci(-arcsin(aa(x)/K1)+theta)*K1*K2*cos(theta)+Si (-arcsin(aa(x)/K1)+theta)*K1*K2*sin(theta)+x = _C1
Je doute qu'on puisse expliciter a'(t), donc encore moins a(t).
Si θ – K2. a' est toujours proche de 0, on peut utiliser une approximation du sinus pour avoir une équa diff approchée d'inconnue a', mais l'intégration qu'il faudra faire sera très sensible aux erreurs.
Peut-être une intégration approchée de l'équa diff ?
Cordialement.
Merci pour votre réponse ultra rapide.
J'ai omis de préciser que a=0 et a'=0, quand t=0. Cà peut aider?
Non, ce sont des conditions initiales, elles ne donnent pas d'outil pour la résolution exacte. Par contre, pour une résolution approchée, c'est très utile.
Merci d'avoir essayé de m'aider.
J'ai pu approcher suffisamment la solution grace à EXCEL en calculant a" initial dans la première ligne (en prenant a' = 0)
puis, ligne par ligne en les incrémentant de 5ms, j'ai pu y calculer a' et a", d'où finalement a(t)
