Bonjour j'espère que vous allez bien.
Voici la question sur laquelle je suis coincé.
Avez-vous une idée svp ?
Comme c'est la variance estimée elle est légèrement plus petite que celle observée qui vaut 59.81?
Pouvez-vous m'aider svp?
J'ai essayé sans succès
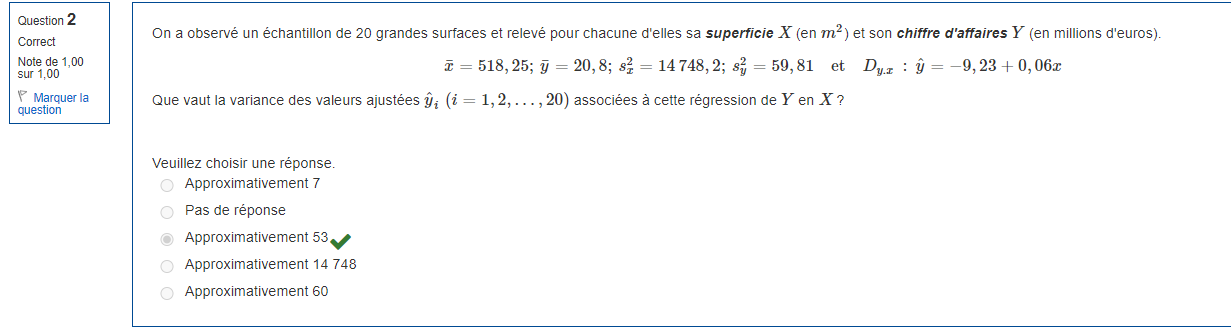
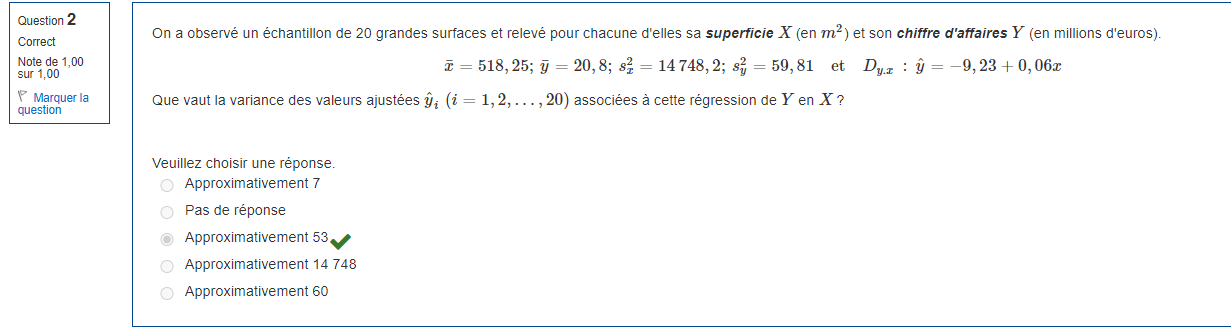
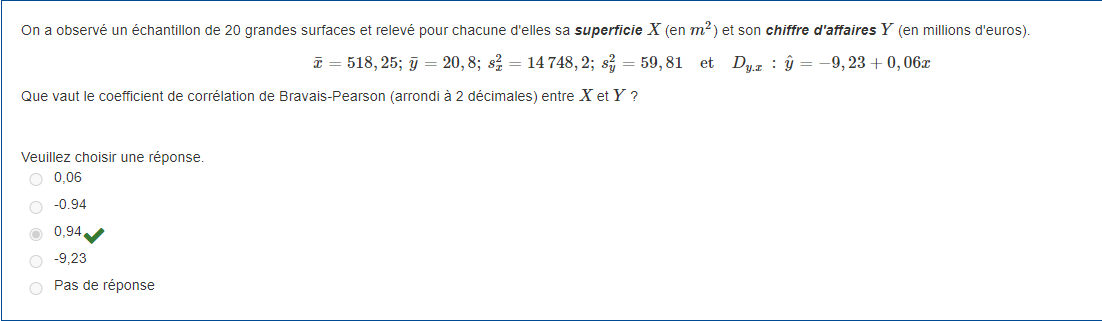
Pour calculer la variance des valeurs ajustées ŷi, nous utiliserons la formule suivante :
Var(ŷi) = s²y * (1/n + (xi - x̄)² / ∑(xi - x̄)²)
où :
s²y est la variance de Y (59,81)
n est la taille de l'échantillon (20)
xi est la valeur de la variable X pour l'observation i
x̄ est la moyenne des valeurs de X (518,25)
En utilisant les valeurs fournies, nous pouvons calculer la variance des valeurs ajustées ŷi :
Var(ŷi) = 59,81 * (1/20 + (xi - 518,25)² / ∑(xi - 518,25)²)
La somme ∑(xi - 518,25)² peut être calculée en utilisant les informations de la variance de X (14748,2).
Var(ŷi) = 59,81 * (1/20 + (xi - 518,25)² / (20 * 14748,2))
Cependant, nous n'avons pas la valeur spécifique de xi, il est donc impossible de calculer la variance des valeurs ajustées sans connaître les valeurs individuelles de X dans l'échantillon.
-----