Salut, j'espère que vous allez bien
Vous pouvez faire une rédaction pour cet exercice
On considère l'équation différentielle suivante :
x^2.y'+y=x.
1) déterminer une solution formelle au voisinage de zéro de la forme : f^(x)=x^landa.somme de n>0(a_n×x^n) ; ou landa un réel,a_n un réel , que l'on détermine.
2)montrer que f^(x) est de type Gevrey.
3) calculer la transformée de Borel de f^(x).
-----




 il suffit de ré-écrire sous la forme
il suffit de ré-écrire sous la forme  voir maintenant
voir maintenant
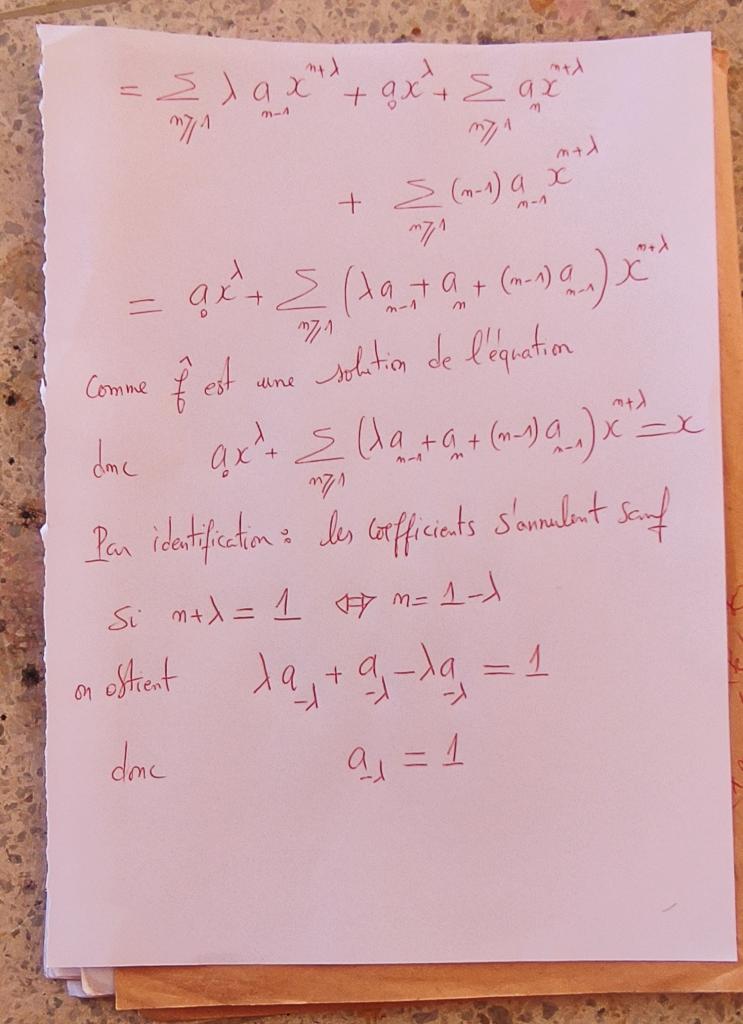
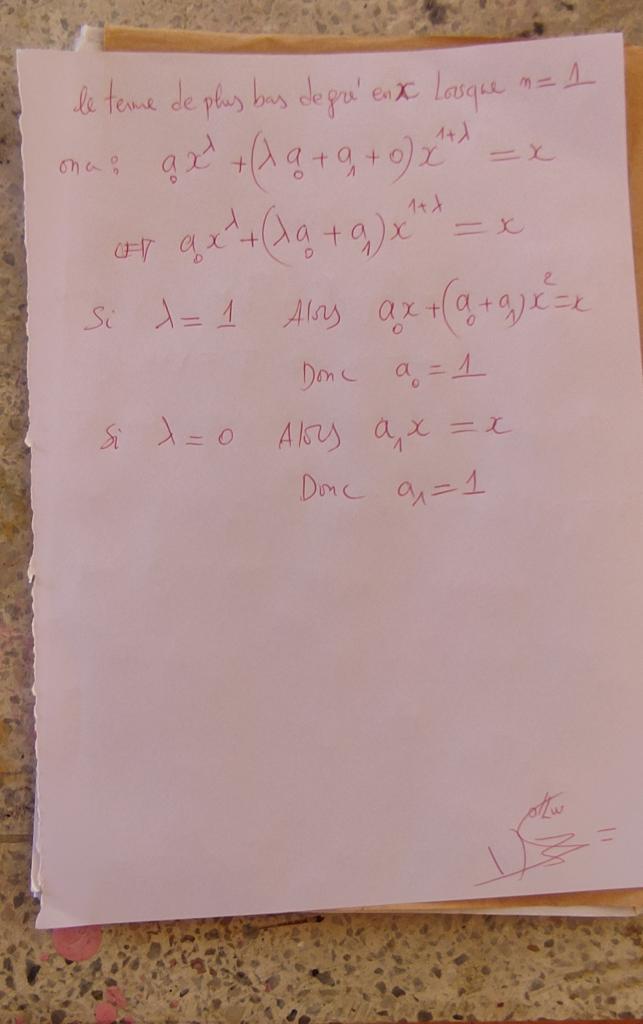 et ceci
et ceci

 par identification n'est ce pas
par identification n'est ce pas