Coordonées GPS projection en coordonées cartésiennes

[mweber]

Bonjour,

En cherchant sur le net je n'ai pas vraiment trouvé de réponse à mon problème, pourtant il doit en intéresser plus d'un :


Je prends du ciel une photo d'un terrain de 50 m de coté, par exemple avec un drone ou à partir d'une une image satellite.

On considère la distorsion géométrique de l'image comme négligeable. (Ou du moins corrigeable)

La photo fait X * Y pixels, et n'est pas forcément orientée au nord (ni les bords du terrain d'ailleurs)

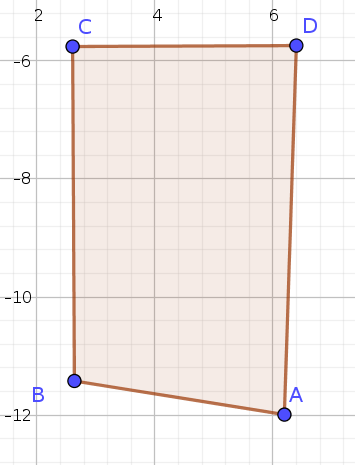
Aux 4 coins de cette image (par exemple), on relève précisément les coordonnées GPS (On peu au besoin faire d'autres mesures dans divers points de l'image, ayant des points remarquables par exemple: un poteau électrique...).

J'aimerai à partir de là, pour une position GPS donnée (système standard géodésique WGS 84), obtenir les coordonnées X et Y correspondantes de mon image.

L'idée est de positionner un robot avec un GPS RTK Centipède, dont la précision peut être de quelques centimètres.

Pour être raisonnable, la résolution de l'image (et donc la grille de positionnement) pourrait être environ de 10 cm par pixels.

Je ne suis pas très fort en maths mais plutot en info / élec..

Si cela vous intéresse, j'ai réussi à mettre en œuvre avec un microcontrôleur ESP32 et une carte GPS Ubox à base de module ZED-F9P, un récepteur de cette précision.
Pour environ 150 € de matériel. (Il n'y a aucun abonnement ou inscription pour bénéficier du service RTK Centipède)

https://docs.centipede.fr/#:~:text=C...ire%20continu.

https://fr.aliexpress.com/item/10050...yAdapt=glo2fra

(je me suis d'ailleurs rendu compte que les cartes Google Map ont un décalage de 1 m par rapport à la réalité chez moi (près de Nantes)

Merci pour votre aide !

Matthieu
-----

[jiherve]

bonjour
coordonnées X,Y ok mais dans quel référentiel ?
JR

[mweber]

Le zéro X et Y en bas à droite de l'image par exemple ?

[Biname]

Des logiciels font ça, le mot clé est en anglais "raster", "rasterisation". Tu cliques sur deux points de ton image et tu en donnes les coordonnées GPS et des coordonnées seront affectées à tous les autres points de l'image.

[A voir en vidéo sur Futura]

[GBZM]

Bonsoir,

Je ne comprends pas très bien le problème.
Est-ce que ça a à voir avec ça ?
https://www.geogebra.org/m/q7gvkmeq

[mweber]

Humm... Je vais vous faire un schéma ce sera beaucoup plus simple à comprendre (mais peut être pas à résoudre)

Je fais 6 relevés GPS précis sur la carte ci-dessous (Relevés GPS 1 à 6) Les relevés 5 et 6 étant facultatifs.
Ils sont liés à une position x,y correspondante dans l'image

la croix jaune représente un véhicule équipé d'un GPS
Je voudrais connaitre sa position x,y.

Attention : ne pas tenir compte de l'image affichée mais cliquer sur le lien carte2.png car paint m'a conservé une partie en haut que je ne voulais pas garder !
carte2.png

[Gyrocompas]

Bonjour,
Eviter de se compliquer la situation.
Rester dans la logique d'un géomètre, tout point se définit depuis une situation réputée précise X, Y.
La différence x et y du point recherché donne ses coordonnées (X+x, Y+y).

Exemple récent, besoin de définir les positions exactes des supports d'un rail de sécurité sur une portion de route nouvelle.
Sa station a été positionnée avec précision.
Ensuite, en utilisant le réflecteur laser d'une mire, il a été capable de positionner chaque support depuis une table calculée au préalable.

Une position déduite d'une image nécessite de connaître les positions des 2 points extrêmes situés sur sa diagonale.
A partir de là, il est facile de définir la résolution x et y de chaque pixel.
La taille du point visé a de forte chance de couvrir plusieurs pixels, ce qui relativise le besoin de précision.

[jiherve]

bonjour
vu les distances pas la peine de se prendre le chou avec des projections!
on suppose x = f(L,G) et y = g(L,G) avec f et g du premier degré
x0 = ax*L0+bx*G0,y0 = ay*L0+by*G0
x1 = ax*L1+bx*G1,y1 = ay*L1+by*G1
x2 = ax*L2+bx*G2,y2 = ay*L2+by*G2
x3 = ax*L3+bx*G3,y3 = ay*L3+by*G3
système à résoudre par les moindres carrés type Cholesky .
JR

[Biname]

La géométrie sphérique permet de calculer la distance entre deux points de la surface terrestre en fonction de leurs coordonnées et du rayon terrestre.
Avec "distance entre deux points terrestres" ou mieux "orthodromie" ou "orthodromic" en anglais, on trouve
https://fr.wikipedia.org/wiki/Orthodromie
Tu devrais aussi trouver des librairies pour python, javascript, ... ???
https://gist.github.com/jeromer/1883777

[Biname]

Il y a une solution python matplotlib selon gpt (en 2 minutes, pas testé)

 Cliquez pour afficher

import matplotlib.pyplot as plt
from matplotlib.image import imread

def rasterize_image(image_path, latitudes, longitudes, figsize=(10, 10)):
    """
    Rasterize an image based on given latitudes and longitudes.

    Args:
    - image_path (str): Path to the image file.
    - latitudes (list): List of latitude coordinates.
    - longitudes (list): List of longitude coordinates.
    - figsize (tuple): Figure size.

    Returns:
    - None
    """
    # Load image
    img = imread(image_path)

    # Create figure
    plt.figure(figsize=figsize)

    # Plot image
    plt.imshow(img, extent=(min(longitudes), max(longitudes), min(latitudes), max(latitudes)))

    # Set labels
    plt.xlabel('Longitude')
    plt.ylabel('Latitude')

    # Show grid
    plt.grid(True)

    # Show plot
    plt.show()

# Example usage
if __name__ == "__main__":
    image_path = 'path/to/your/image.jpg'  # Replace with your image path
    # Example coordinates
    latitudes = [40.7128, 41.8781, 34.0522]
    longitudes = [-74.0060, -87.6298, -118.2437]
    rasterize_image(image_path, latitudes, longitudes)

[mweber]

Ok merci !

Tout à fait, seuls 2 relevés GPS en diagonale suifferaient à "calibrer" la carte (par ex le N°1 et le N°4)

En appliquant la fonction calculate_orthodromic_distance () décrite dans github: https://gist.github.com/jeromer/1883777
Je vois que je peux m'en sortir en l'appelant 2 fois en faisant une projection sur l'axe des x puis sur l'axe des y pour connaitre la distance par rapport au coin de l'image.
Bien entendu, au tout début, il me faut calculer avec cette même fonction la longueur (en mètres...) représentant l'axe x de l'image et la longueur y

vu les distances pas la peine de se prendre le chou avec des projections!
on suppose x = f(L,G) et y = g(L,G) avec f et g du premier degré
x0 = ax*L0+bx*G0,y0 = ay*L0+by*G0
x1 = ax*L1+bx*G1,y1 = ay*L1+by*G1
x2 = ax*L2+bx*G2,y2 = ay*L2+by*G2
x3 = ax*L3+bx*G3,y3 = ay*L3+by*G3
système à résoudre par les moindres carrés type Cholesky .
JR

Heu, désolé comme dis plus haut je ne suis pas une flèche en maths
Que représente L et G.
Jamais joué avec les moindres carrés...

Merci !
Matt

[Biname]

Ok merci !

Tout à fait, seuls 2 relevés GPS en diagonale suifferaient à "calibrer" la carte (par ex le N°1 et le N°4)

En appliquant la fonction calculate_orthodromic_distance () décrite dans github: https://gist.github.com/jeromer/1883777
Je vois que je peux m'en sortir en l'appelant 2 fois en faisant une projection sur l'axe des x puis sur l'axe des y pour connaitre la distance par rapport au coin de l'image.
Bien entendu, au tout début, il me faut calculer avec cette même fonction la longueur (en mètres...) représentant l'axe x de l'image et la longueur y

Merci !
Matt

Il te faudra trouver un rayon terrestre ou un mile nautique plus précis que celui du code pour améliorer la précision, ici 1/1852e ... à voir !

[albanxiii]

Il y a une solution python matplotlib selon gpt (en 2 minutes, pas testé)

 Cliquez pour afficher

import matplotlib.pyplot as plt
from matplotlib.image import imread

def rasterize_image(image_path, latitudes, longitudes, figsize=(10, 10)):
    """
    Rasterize an image based on given latitudes and longitudes.

    Args:
    - image_path (str): Path to the image file.
    - latitudes (list): List of latitude coordinates.
    - longitudes (list): List of longitude coordinates.
    - figsize (tuple): Figure size.

    Returns:
    - None
    """
    # Load image
    img = imread(image_path)

    # Create figure
    plt.figure(figsize=figsize)

    # Plot image
    plt.imshow(img, extent=(min(longitudes), max(longitudes), min(latitudes), max(latitudes)))

    # Set labels
    plt.xlabel('Longitude')
    plt.ylabel('Latitude')

    # Show grid
    plt.grid(True)

    # Show plot
    plt.show()

# Example usage
if __name__ == "__main__":
    image_path = 'path/to/your/image.jpg'  # Replace with your image path
    # Example coordinates
    latitudes = [40.7128, 41.8781, 34.0522]
    longitudes = [-74.0060, -87.6298, -118.2437]
    rasterize_image(image_path, latitudes, longitudes)

Question sérieuse : quel est l'intérêt de ce message ?

[GBZM]

Bonjour,
Quelques remarques :
1°) il y a visiblement quelque chose qui cloche avec les y indiqués sur la carte : les y=296 du relevé 5 et y=550 du relevé 6 ne vont pas avec les y=800 des relevés 3 et 4
2°) si on représente les coordonnées GPS des quatre coins de l'image, on n'obtient pas du tout un rectangle, mais ça :

3°) Vu les dimensions du terrain, se préoccuper du rayon de la terre ou je ne sais quoi est complètement illusoire.
Serait-il possible de vérifier les données ?
Est-ce que le terrain photographié est plan ? (pas forcément horizontal, mais plan)
Si les coordonnées GPS des quatre coins de l'image sont correcte, alors il y a une déformation de perspective.

[GBZM]

@mweber : Quand tu as rogné le haut de l'image, tu as oublié de soustraire ce qu'il faut (environ 136) aux y des relevés GPS 3,4,5,6.

Je suis reparti de la carte non rognée pour trouver une transformation affine par la méthode des moindres carrés à partir des 6 relevés.
coord X,Y sur l'image non rognée = M * coord GPS tronquées + T
(par coord GPS tronquées, je veux dire que je garde les 4 dernières décimales de la 1e coordonnée et les 5 dernières de la 2e, par exemple [4243,7241] pour le relevé 6).
Je trouve, pour la matrice M et le vecteur de translation T

M=[[ 0.00772209 -0.11712931]
[-0.17977242 -0.00259935]]

T=[[1244.99578087]
[1336.68281697]]

en appliquant ça à la position GPS du rover, je trouve (313,466) au lieu du (310,473) lu sur l'image non rognée.

Je vais voir si on a un meilleur résultat en prenant en compte la déformation de perspective. Ce n'est plus alors une transformation affine. Mais avant j'attends confirmation des données GPS pour les quatre coins de l'image rognée.

[mweber]

Oui tout à fait !

L'image donnée est juste un exemple pour montrer le principe de ce que je cherche à obtenir !

...exemple par là imprécis car réalisé sans aller sur le terrain, juste en cliquant sur Google map et sans forcément arriver à bien viser avec la souris (j'aurai finalement dû le préciser) de plus, j'ai un un bug avec paint qui n'affichait pas le haut de l'image d'où le décalage (d'environ 136 pixels en y).

On est d'accord, les coordonnées latitude et longitudes aux coins doivent avoir une de leur valeur identique !

[mweber]

On est d'accord que l'idée c'est :

On a un algorithme (le coder en C++ sur un microcontrôleur je sais faire)

- On lui fourni 2 coordonnées GPS correspondant au coins (haut, gauche) et (bas, droite) du terrain et qui collent à l'image satellite de ce terrain.

- On indique à quelles coordonnées x,y (en pixels) ces 2 coordonnées GPS correspondent dans l'image donc ici: 0,0 pix et 700,800 pix (image que l'algo n'a pas besoin de connaitre, mis à par ses dimensions en pixels évidemment)

L'algo détermine: la largeur et la longueur du terrain et donc la "taille" d'un pixel x et d'un pixel y


Maintenant à chaque fois que je le souhaite :
Je peux demander à une fonction de l'algo de me renvoyer la position x,y correspondant à une coordonnée GPS entrée en argument.

Et oui, ici on peu simplifier (je pense) les calculs complexes vu que le terrain ferait max 50 x 50m

[GBZM]

Je fais 6 relevés GPS précis sur la carte ci-dessous

Tu nous as donc raconté des bobards ...
Le calcul de redressement de perspective avec les coordonnées GPS des 4 coins de l'image donne un résultat assez mauvais ... normal puisque ces coordonnées GPS sont fantaisistes.
Reste le calcul de la transformation affine.

Un code en python :

import numpy as np

GPS=np.array([[6449,11255],[2893,10686],\
     [2863,5023],[6651,5006],[5706,8398],[4243,7241]])
XY=np.array([[0,136],[0,800],[700,800],[700,136],\
             [292,296],[424,550]])

def Aff(P,Q) :
    eq=np.concatenate((P,np.ones((len(P),1))),axis=1)
    teq=np.transpose(eq)
    L1=np.linalg.solve(teq@eq,teq@XY[:,0])
    L2=np.linalg.solve(teq@eq,teq@XY[:,1])
    L=np.stack((L1,L2))
    return L[:,:2], L[:,2]

M,T= Aff(GPS,XY)
print(M)
print(T)

[[ 0.00772209 -0.11712931]
[-0.17977242 -0.00259935]]
[1244.99578087 1336.68281697]

print(np.round(M@np.array([4725,8266])+T))

[313. 466.]

[mweber]

Ok merci,

Bon c’était juste un exemple que j'ai fait vite fait pour expliquer le problème pas pour s'en servir comme référence absolue

Par contre pas possible de coder en python et encore moins avec la lib Pinema

Ca donnerai ca en Arduino (Ok on glisse ici un peu du forum maths au forum info, mais ...)

Programme à tester, pas sur du résultat pour le moment

// Définition d'une structure pour représenter une matrice 2x2
struct Matrix2x2 {
    float data[2][2];
};

// Définition d'une fonction pour inverser une matrice 2x2
Matrix2x2 inverse(Matrix2x2 mat) {
    float determinant = mat.data[0][0] * mat.data[1][1] - mat.data[0][1] * mat.data[1][0];
    Matrix2x2 invMat;
    invMat.data[0][0] = mat.data[1][1] / determinant;
    invMat.data[0][1] = -mat.data[0][1] / determinant;
    invMat.data[1][0] = -mat.data[1][0] / determinant;
    invMat.data[1][1] = mat.data[0][0] / determinant;
    return invMat;
}

// Définition d'une fonction pour multiplier une matrice 2x2 par un vecteur 2x1
Matrix2x1 multiply(Matrix2x2 mat, Matrix2x1 vec) {
    Matrix2x1 result;
    result.data[0] = mat.data[0][0] * vec.data[0] + mat.data[0][1] * vec.data[1];
    result.data[1] = mat.data[1][0] * vec.data[0] + mat.data[1][1] * vec.data[1];
    return result;
}

// Fonction pour effectuer la transformation affine
Matrix2x2 Aff(Matrix2x2 P, Matrix2x2 Q) {
    Matrix2x2 eq;
    // Concaténation de la matrice P avec une colonne de 1 supplémentaire
    eq.data[0][0] = P.data[0][0]; eq.data[0][1] = P.data[0][1]; eq.data[0][2] = 1;
    eq.data[1][0] = P.data[1][0]; eq.data[1][1] = P.data[1][1]; eq.data[1][2] = 1;

    // Calcul de la transposée de la matrice eq
    Matrix2x3 teq;
    for (int i = 0; i < 3; ++i) {
        for (int j = 0; j < 2; ++j) {
            teq.data[i][j] = eq.data[j][i];
        }
    }

    // Conversion de la matrice Q en une matrice 2x1
    Matrix2x1 XY;
    XY.data[0] = Q.data[0][0];
    XY.data[1] = Q.data[1][0];

    // Résolution du système d'équations linéaires
    Matrix2x1 L1 = multiply(inverse(multiply(teq, eq)), multiply(teq, XY));

    XY.data[0] = Q.data[0][1];
    XY.data[1] = Q.data[1][1];

    Matrix2x1 L2 = multiply(inverse(multiply(teq, eq)), multiply(teq, XY));

    // Construction de la matrice de transformation finale
    Matrix2x2 L;
    L.data[0][0] = L1.data[0]; L.data[0][1] = L2.data[0];
    L.data[1][0] = L1.data[1]; L.data[1][1] = L2.data[1];
    return L;
}

void setup() {
    Serial.begin(9600);

    Matrix2x2 GPS = {{6449, 11255}, {2893, 10686}, {2863, 5023}, {6651, 5006}, {5706, 8398}, {4243, 7241}};
    Matrix2x2 XY = {{0, 136}, {0, 800}, {700, 800}, {700, 136}, {292, 296}, {424, 550}};

    Matrix2x2 M = Aff(GPS, XY);

    Serial.println("M:");
    for (int i = 0; i < 2; ++i) {
        for (int j = 0; j < 2; ++j) {
            Serial.print(M.data[i][j]);
            Serial.print("\t");
        }
        Serial.println();
    }
}

void loop() {}

[GBZM]

Bizarre ...
Les matrices qui interviennent ne sont pas que des matrices 2x2. En particulier la matrice eq est une matrice 6x3.
Ma fonction Aff(P,Q) prend deux listes de points de même longueur, P et Q, et retourne la transformation affine qui envoie P le plus proche possible de Q, au sens des moindres carrés.
Je m'aperçois que j'avais laissé traîner des XY. Je corrige :

def Aff(P,Q) :
    eq=np.concatenate((P,np.ones((len(P),1))),axis=1)
    teq=np.transpose(eq)
    L1=np.linalg.solve(teq@eq,teq@Q[:,0])
    L2=np.linalg.solve(teq@eq,teq@Q[:,1])
    L=np.stack((L1,L2))
    return L[:,:2], L[:,2]

[Biname]

Ne serait-il pas préférable de créer une carte à partir des données GPS, plutôt que l'inverse ? Points extrêmes N(lon, lat), S(lon, lat), O(lon, lat), E(lon, lat). Axe des x en S_lat, axe des y en O_lon, pour obtenir des coordonnées locales, on fait simplement LOCAL(GPS_lon - O_lon) * k,(GPS_lat - S_lat) * k)), k permettant de régler l'échelle et la taille des pixels sur le terrain. Ensuite, on crée une table des points comportant un ou deux bytes donnant des infos sur ce points. L'adresse d'un point dans la table est LOCAL_x * LOCAL_y

Pour 100m * 100m avec des "pixels/résolution" de 10cm, il suffit de 1 mégaoctets, pour 1 byte d'infos par point.

[Biname]

LOCAL_X * LOCAL_Y est à revoir mais c'est simple.

[mweber]

Pas bête,

La carte satellite permettait de pouvoir connaitre de visu les obstacles (c'est un robot tondeuse) mais vu que les cartes Google map et autre sont pas assez précises (décalage des coordonnées), c'est pas forcément pratique
Et donc tu as peut être LA solution !
Quitte à reconnaitre et à faire apprendre au robot sur le terrain les zones interdites qui seront enregistrée dans ce fichier.

Dans ton exemple, "LOCAL" c'est une fonction ?

Merci
Matt

[Biname]

LOCAL_X = (GPS_lon - O_lon) * k, c'est très simple, yakade calculer k et de tenir compte des signes lon/lat
LOCAL_Y = (GPS_lat - O_lat) * k angle décimaux

L'idéal serait de reprendre le format bitmap pour les pixels, mais le mieux nuit au bien.

[Biname]

cor si pas faite : LOCAL_Y = (GPS_lat - S_lat) * k angle décimaux

[Gyrocompas]

Bonjour,
Envisager de revoir la méthode de guidage.
Utiliser ses coordonnées pour suivre une tondeuse nécessite une précision 'diabolique'.
Par exemple, à la latitude du lieu, quelle doit être la précision pour garantir 1m de résolution en longitude.

Délimiter les limites du terrain à traiter, l'engin se repositionne par rapport à ces repères.
Une précision de l'ordre de 10 cm peut être atteinte.