Bonjour,
j'ai rencontré le problème suivant, c'est problème réel suite à une création d'échantillons:
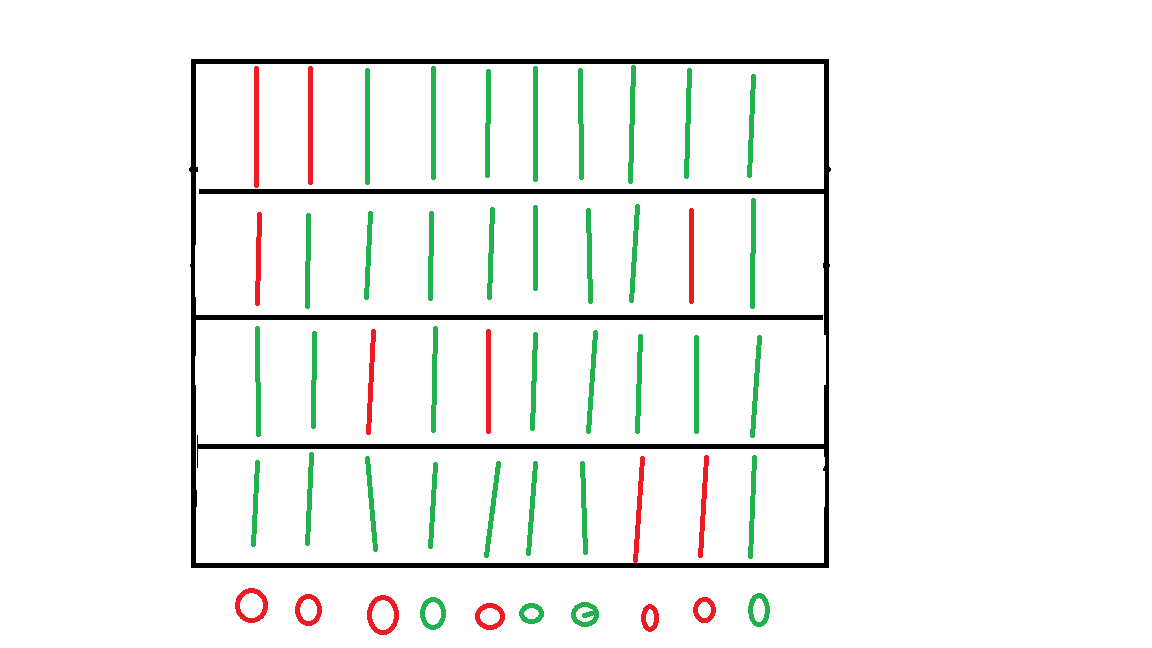
Nous avons une pièce d'une épaisseur donnée avec des trous qui peuvent être occlus ou non. La probabilité qu'ils soient occlus est une fraction entière de dixième. 2/10 par exemple.
Maintenant nous souhaitons avoir la probabilité ici l'espérance qu'un trou soit occlus pour une épaisseur supérieure: par exemple quatre fois l'épaisseur initiale.
Je vous donne un schéma -certes maladroit-mais vous comprendrez. Les cercles en bas représentent le résultat pour une colonne totale. Puisqu'il suffit que le passage soit une fois occlus ou même s'il l'est plusieurs fois, cela ne compte que pour "un".
Alors je suis relativement novice en combinatoire et je pêche... Pour simplifier le problème j'ai essayé de ne pas réfléchir en probabilités mais en combinaisons/arrangements. On comprend que sur la hauteur totale le cylindre peut être occlus 2,3,4,5,6,7 ou 8 fois selon les combinaisons.
J'ai beau sommer les combinaisons des différentes possibilités (2,3,4,5,6,7 ou 8 occlusions) pourtant je ne trouve pas le même nombre de combinaisons que la combinaison totale -Arrangements de (2 parmi 10)^4
Et donc mon espérance est nécessairement fausse. Je veux multiplier chaque "probabilité" par son nombre d'occlusion totale : P(2)*0.2+P(3)*0.3 +P(4)*0.4...etc. pour obtenir l'espérance. Quelle démarche prendre ici? J'ai bien raison de raisonner en arrangements?
-----