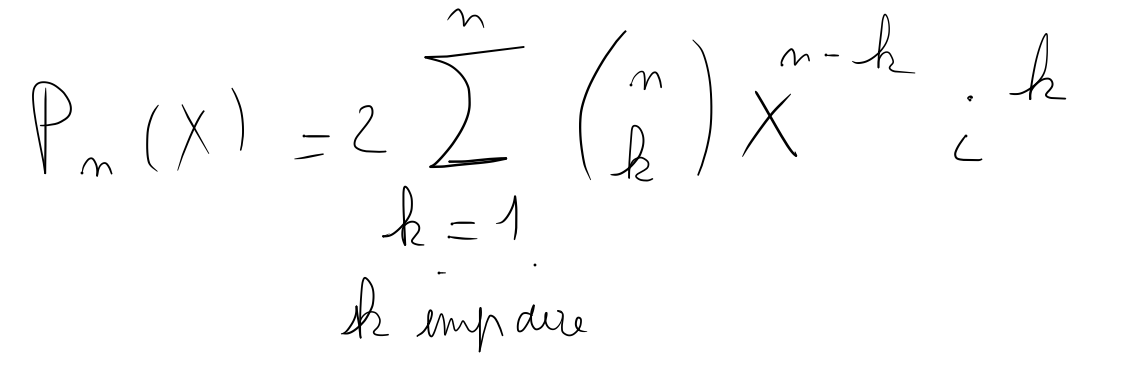Factorisation Polynôme

[vall]

Bonjour à tous,

Je cherche à factoriser le polynôme P_n(X) = (X+i)ⁿ - (X-i)ⁿ dans R[x] et C[X] et ce pour tout entier n non nul.

J'ai essayé de développé pour les cas n = 1,2,3 afin de conjecturer une potentielle formule puis la démontrer par récurrence mais rien à faire :
P₁(X) = 2i
P₂(X) = 4iX
P₃(X) = 6i(X-1/sqrt(3))(X+1/sqrt(3))

J'ai également développé les deux polynômes (X+i)ⁿ et (X-i)ⁿ à l'aide du binôme de Newton puis fais la différence pour obtenir la formule suite :


Si quelqu'un a un conseil ou la solution je suis preneur !

Merci beaucoup et bonne journée.
-----

Publicité

[gg0]

Bonjour.

Quelques remarques :

* Pour factoriser dans R[X], il faut que le polynôme soit à coefficients réels. Ta formule de développement n'a pas trop d'intérêt, sauf justement pour voir que Pn n'est pas dans R[X].
* Cependant, en posant Qn(X)=Pn(X)/i, on peut se poser la question de factoriser Q dans R[X] et dans C[X].
* La factorisation est classique quand on connaît les racines (réelles pour R[X]) et le coefficient dominant. Le coefficient dominant, tu l'as, pour les racines, il te suffit de résoudre Pn(X) =0 soit (X+i)^n=(X-i)^n.
* On pourra se ramener aux racines n-ièmes de l'unité.

Cordialement.