Probabiltés - Jeu à cliquets

[Nekama]

En posant :
n(i) : nombre de parties nécessaires pour atteindre le score de 10 en partant de l'état (i)
K : variable aléatoire qui vaut i+1 avec une probabilité 1/2 et i-1 avec une probabilité 1/2

On a : n(i) = 1 + n(K)

On peut alors écrire :

E[n(i)] = E[1] + E[n(K)] avec E[n(K)] = 1/2 E[n(i+1)] + 1/2 E[n(i-1)] ce qui ramène à l'équation utilisée par BlackJack : m_i+1 - 2 m_i + m_i-1 = -2

Var[n(i)] = E[n(i)^2] - E[n(i)]^2 = s_i - m_i^2 et l'équation : s_i+1 - 2 s_i + s_i-1 = -2 -2 (m_i+1 + m_i-1) qui peut se simplifier avec la résolution de la précédente.

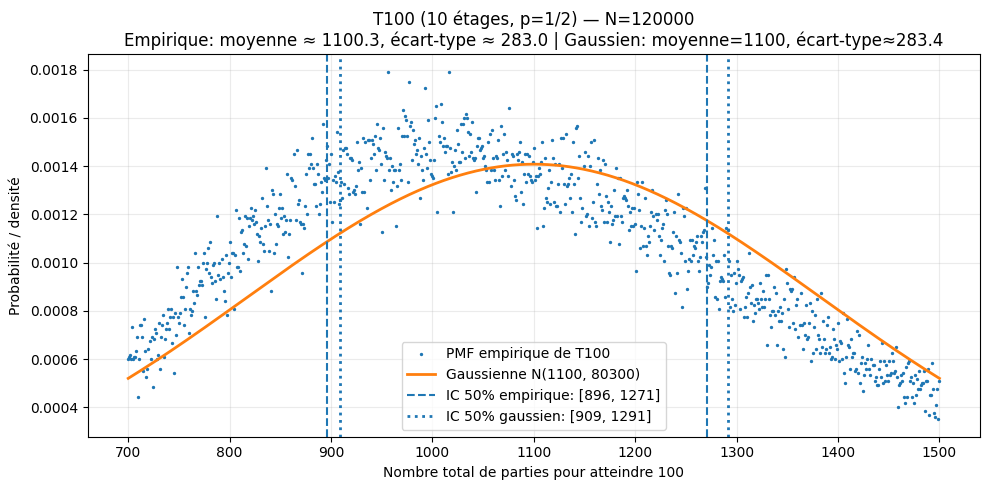
On peut résoudre les 2 équations avec les conditions de bords et il suffit alors de poser i = 0 pour trouver la réponse à la question pour un set de 10 parties.

Pour les 10 sets de 10 parties, la moyenne est multipliée par 10 et l'écart type par racine(10).

L'intervalle de confiance se détermine selon la % de confiance recherché (pour 50 %, z = 0,675)
-----

[GBZM]

Heu ... pour la variance, c'est multiplier par non ? C'est la variance de la somme de 10 variables iid.

Voyons, Gérard, ne confondrais-tu pas variance et écart-type ? La variance de la somme de variables aléatoires indépendantes est la somme des variances.

[gg0]

Oui, effectivement.
C'est amusant, parce que cette multiplication par 10 était mon idée initiale (message #2), puis que j'ai eu un doute qui m'a poursuivi au point de ne pas lire ce que j'ai écrit pour "bien réfléchir" : V(X)=10V(X1) !!!
Fait pas bon vieillir ..

[GBZM]

Aux amateurs du 0,675 (Nekama et Black Jack) : vous supposez que la variable aléatoire "Temps d'atteinte de 100" est gaussienne, pour employer la table de la loi normale. Elle est peut-être pas trop loin d'une gaussienne, mais comme ce n'est la somme que de 10 v.a. i.i.d., l'approximation n'est peut-être pas terrible.
Si on veut ceinture et bretelles, on peut utiliser Bienaymé-Tchebychev et multiplier l'écart-type par au lieu de 0,675.

[Nekama]

Le TCL n'est pas applicable sur une somme de 10 variables aléatoires.
Mais on demande un intervalle de confiance à 50 % pour une distribution assez symétrique autour de sa moyenne.

Au final, ce n'est "pas mal".
Tchebichev a de très grandes bretelles