Ecoulement laminaire sur un plan incliné

[kira974]

Bonjour a tous, voici mon problème :

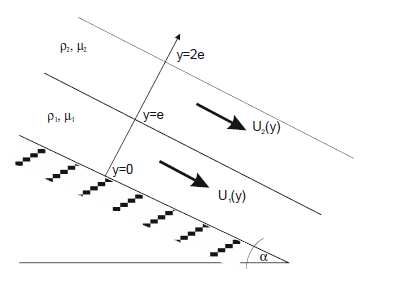
Une couche mince de fluide ( viscosité n et masse volumique p) d'épaisseur e, coule le long d'un plan incliné, dont la ligne de plus grande pente fait un angle alpha avec l'horizontale.
Le champs des vitesses, supposé indépendant du temps, est de la forme V=V(y) suivant le vecteur Ux

Comment déterminer la forme V(y) ainsi que pour une largeur L la relation entre l'épaisseur et le débit massique D?

J'aimerais également savoir comment calculer la vitesse maximale pour e=1mm et alpha=45° dans le cas ou n=1.10^-3 Pa.s et p=1.10^3kg/m^3

[erff]

Bonjour,

Il te suffit d'utiliser l'équation de Navier - Stokes en régime permanent.

Tu noteras que le terme convectif n'intervient pas. On a l'équation :



Sachant que :

Il te reste à projeter l'equation de NS sur Ux et Uy..


Tu auras 2 conditions aux limites : V(y=0)=0 (le fluide adhère au plan incliné)
dV/dy(e)=0 (l'atmosphère n'exerce aucun effort tangentiel sur le fluide)


EDIT : il y a de grandes chances qu'on néglige le terme (grad(p) en raisonnant en ordre de grandeur)

[kira974]

comment sait on que l'on est en régime permanent et que le terme convectif n'intervient pas. ?
De plus lorsque que je porjette mon équation suivant Uy je n'ai plus de terme faisant intervenir la vitesse est normal?

[erff]

comment sait on que l'on est en régime permanent et que le terme convectif n'intervient pas

Régime permanent car :

Le champs des vitesses, supposé indépendant du temps...

Terme convectif n'intervient pas car :
en effectuant le calcul tout simplement.

De plus lorsque que je porjette mon équation suivant Uy je n'ai plus de terme faisant intervenir la vitesse est normal?

Oui c'est normal, la projection sur Uy va te permettre de trouver des trucs sur la pression, tu verras notamment qu'on pourra la supposer constante car :

étant donné que