Bonjour,
je me tourne par ici pour trouver un peu d'aide pour un problème peut-être déjà résolu.
Je cherche à trouver une solution analytique pour ce problème :
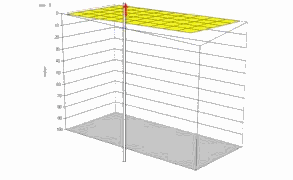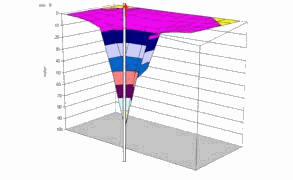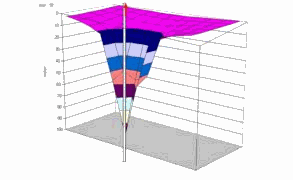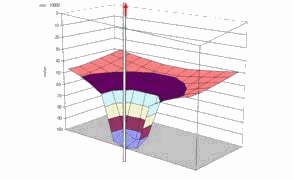
Dans une cuve dont les dimensions sont 1x1x1 m remplie de sable, nous avons disposé un puits crépiné sur toute la hauteur h de sable au centre de la cuve.
Techniquement ce système représente un ensemble cloisonné par 5 parois imperméables (les 4 côtés de la cuve + le fond).
La recharge en eau se faisant par le dessus (pluie) nous cherchons à exprimer le débit s'écoulant par le fond du puits ainsi que la hauteur du niveau de l'eau en fonction de la distance au puits.
Dans la bilbiographie, ceci se rapproche à un essais par pompage
où le débit est exprimé par l'expression de Dupuit-Forchheimer :
Q=pi.K.(H²-h²)/ln (R/r)
avec Q le débit, K la conductivité hydraulique, H la hauteur initiale saturée, h la hauteur aux environs du puits (influencée par le cone de rabattement), R le rayon d'influence enfin r le rayon efficace du puits.
Cette expression représente le débit arrivant au puits.
Concrètement le débit passant dans le puits est d'après Kozeny "suintement" :
Q=2pi.r.h.K
avec h la différence de hauteur entre la première goutte "haute" qui entre dans le puits et le fond du puits évacuant l'eau.
Ce qui me pose problème c'est que pour les résolutions de ces équations, nous sommes en régime permanent, et dans mon cas ce n'est pas le cas (puisque le débit varie en fonction du niveau d'eau qui varie lui aussi puisqu'il n'y a pas d'alimentation permanente sur les bords de cuve).
J'ai trouvé cette image qui représente assez bien le problème au détail prêt que c'est une vidange par un puits, mais il n'y avait pas d'équation associée :
merci pour votre aide !
-----