Les Forces: Relation entre tension et l'angle alpha

[invite5c47911b]

Bonjour, Je suis un etudiant libanais en classe de seconde, j'ai demain un examen de physique, mais je n'arrive pas a comprendre la relation entre l'angle alpha, et la tension du fil et les autres forces.
Ici J'aimerais vous demander 2 questions:
1- C'est Quoi Px Py et Rx Ry et pourquoi les utuliser et comment
2- J'essaie de faire un exercice de l'examen passe, mais je me retrouve perdu

Voici L'exercice:

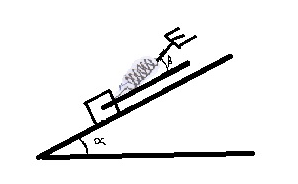
Un Corps A de poids 3N repose sans frottement sur un plan incline d'un angle alpha=30 degres avec l'horizontale. La reaction du plan sur le corps A est perpendiculaire au plan. Ce corps est maintenu sur le plan incline par l'intermediaire d'un ressort faisant un angle BETA avec la ligne de plus grande pente du plan.

1. Faire Le bilan des forces qui s'exercent sur le corps A.
2. En deduire L'intensite de la force T exercee par le ressort A en fonction de l'angle Beta
3. Calculer ||T|| ( AVEC FLECHE VECTEUR, JE NE PEUX PAS LA METTRE LA) pour Beta=0 degres, Beta=30 degres, Beta=60 degres.
4. En Deduire dans chaque cas precedent l'allongement de ce ressort de raideur k=50N/m

Voici Le schema dessine par moi sur PAINT, et l'image originale de l'exo (gribouillee :S)




MERCI D'AVANCE
-----

[LPFR]

Bonjour et bienvenu au forum.
Commençons par le poids de l'objet. Il est vertical. Dessinez ce poids avec une flèche verticale. Cette force est exercée sur le plan incliné. Comme on suppose qu'il n'y a pas de frictions, le plan incliné à une réaction (uniquement) perpendiculaire au plan (dessinez-la). Et cette réaction compense la composante du poids perpendiculaire au plan. Il reste la composante du poids parallèle au plan qui n'est pas compensée. Si on ne fait rien, le poids glisserait le long du plan.
Ce quelque chose c'est le ressort qui va le faire. S'il tire parallèlement au plan, il doit exercer une force égale à celle du poids non compensée et vers le haut.
Si la force du ressort n'est pas parallèle au plan, seule la composante de cette force parallèle au plan devra compenser la composante du poids parallèle au plan.
Dessinez toutes les forces qui agissent sur le poids. Si celui est immobile, cela veut dire que toutes ces forces se compensent: leur somme (vectorielle) doit être zéro. Séparez les composantes perpendiculaires au plan et parallèles au plan. Les perpendiculaires s'annulent entre elles et le parallèles aussi.
Au revoir.

[invite5c47911b]

Merci, je suis en train d'essayer maintenant j'ai un mal a comprendre ce chapitre j'ai trop peur de l'examen de demain, je vais essayer et vous dire mes resultats, MERCI!! (K)

[invite5c47911b]

" le plan incliné à une réaction (uniquement) perpendiculaire au plan (dessinez-la). Et cette réaction compense la composante du poids perpendiculaire au plan. Il reste la composante du poids parallèle au plan qui n'est pas compensée. Si on ne fait rien, le poids glisserait le long du plan. "

Je n'est pas compris cette partie :S

[A voir en vidéo sur Futura]

[invite5c47911b]

Oh, vous me n'avez pas explique comment en tirer un tension a partir d'un angle, ce sujet est VRAIMENT flou pour moi :S

[LPFR]

Oh, vous me n'avez pas explique comment en tirer un tension a partir d'un angle, ce sujet est VRAIMENT flou pour moi :S

Re.
Vous ne tirez pas une tension à partir d'un angle.
Une tension est "une force sans direction" (entre guillemets). Une corde sous tension T exerce une force égale à T dans la direction de la corde.
Si votre ressort est sous une tension T et fait un angle bêta, il exerce une force F = T, dirigée dans la direction du ressort (suivant l'angle bêta).
A+

[invite5c47911b]

Ah, je ne sais pas pourquoi je n'arrive pas a comprendre :S je n'ai pas encore compris, vous pouvez me repondre avec un francais un peu simple? :$

[invite765432345678]

Oh, vous me n'avez pas explique comment en tirer un tension a partir d'un angle, ce sujet est VRAIMENT flou pour moi :S

Prenons un vecteur F dont l'angle avec un plan est égal à alpha. Le plan porte la direction x d'un repère. La perpendiculaire à ce plan porte la direction y de ce repère.

La projection sur le plan de ce vecteur est égale à Fx= F cos(alpha)

La projection sur la perpendiculaire à ce plan est égale à Fy= F sin(alpha).

C'est donc très simple.

Il faut donc exprimer toutes les projections des forces suivant ces deux directions et exprimer le principe que le corps est au repos. Donc la somme de ces forces, que ce soit suivant la direction x ou y, est égale à zéro.

[invite5c47911b]

Je vais prendre un zero demain :S je n'arrive a comprendre rien! :S Si je vais calculer T
je dois considerer:
Tx= T*sin(alpha)
mais si je ne sais Tx comment pourrais-je la calculer?

[invite5c47911b]

Pouvez vous me faire un corrige pour l'exercice? un corrige complet, cela pourra m'aider...
1) Reponse
2) reponse
etc...
MERCI D'AVANCE!

[invite5c47911b]

Okay, j'ai peut etre compris:
1) Tension T
Poids P
Reaction du support N
2) Px= P.Sin(alpha)= 3.sin30=1.5
Tx= T.Sin(Beta)
Px=Tx
donc T.Sin(Beta)=1.5
T= 1.5/sin(Beta)
3) pour (Beta)=0
T=1.5/sin0= IMPOSSIBLE
pour (Beta)=30
T=1.5/sin30=3N
Pour (Beta)=60
T=1.5/sin60=approx. 1.73N
4) Comment Calcule t'on l'allongement du ressort? :S

[invite726932a4]

Salut,

Je suis nouveau sur le forum, et comme je n'ai pas le courage de travailler. Alors...

Alors, je crois comprendre ce qui est flou pour vous... Pour vous, il manque des infos. Je vais essayer de vous montrer que ce n'est pas le cas.

Déjà, que connait-on?
- la direction et la valeur du poids.
- la direction de la réaction du plan incliné, qui parallèle à ce dernier. (parce qu'il n'y a pas de frottement, ce qui n'est normalement pas le cas)
- la direction de la tension exercée par le ressort.

- l'objet est en équilibre !!! C'est à dire que les forces ce compensent.
Qualitativement, ça veut dire que les forces de réaction et de tension vont s'ajuster pour qu'il y ait un équilibre. (dans les limites physiques du sytème bien sûr: le ressort ne peut pas supporter une masse infinie). Rien d'étonnant! Quand le gros Robert s'assoit sur une chaise, la réaction de la chaise s'ajuste aux contraintes que Robert exerce sur la chaise, même s'il se penche. (dans les limites physiques...). En fait, tout ça dépend des liaisons et des répulsions entre les particules, les atomes, les molécules, etc...

Comme les forces se compensent, tu peux mettre les vecteurs bout-à-bout pour former un triangle (traduction géométrique de la somme des forces est nulle à l'équilibre). Connaissant les vecteurs, c'est un triangle dont tu connais la longueur d'un coté et deux angles... le problème peut donc être résolu !

à toi de jouer: trace le triangle !

J'espère, t'avoir aidé à comprendre ce qui se passe.

[invite726932a4]

Tes équations me font mal à la tête, je n'ai déjà pas le courage de travailler...

T, c'est la longueur d'un coté du triangle... pas dur

Et pour la dernière question, je ne sais plus trop mais c'est transparent: k est en N/m... N doit correspondre à la force T et m c'est l'alongement.

Bon courage.

[invite5c47911b]

OHH Ouiiiii, qu'est ce que je pourrais faire avec ce triangle? ou seront les angles alpha et beta?

[invite5c47911b]

Okay, j'ai peut etre compris:
1) Tension T
Poids P
Reaction du support N
2) Px= P.Sin(alpha)= 3.sin30=1.5
Tx= T.Sin(Beta)
Px=Tx
donc T.Sin(Beta)=1.5
T= 1.5/sin(Beta)
3) pour (Beta)=0
T=1.5/sin0= IMPOSSIBLE
pour (Beta)=30
T=1.5/sin30=3N
Pour (Beta)=60
T=1.5/sin60=approx. 1.73N
4) Comment Calcule t'on l'allongement du ressort? :S

4) k=50N/m
donc Allongement= T/k?

[invite726932a4]

"Dessine!" comme disent tous les profs de seconde.

Moi je trouve alpha et 90°- (alpha+bêta) ... mais pôs sûr ! faut dessiner...

[invite5c47911b]

mais qu'est ce que je dois dessiner? ( JE SUIS NUL en Forces :S)
Je n'ai pas aussi comprit qu'est ce que vous voulez dire?!

[invite765432345678]

Après rapide examen, je trouve une erreur !

Tx = T cos (beta)

Si beta=0 cos(beta)=1 et Tx=T (regardez votre dessin !)

Lorsque vous aurez calculé T, alors T=k delta (x) avec k raideur du ressort et delta (x)= allongement nécessaire du ressort pour produire la réaction T du ressort, dont la projection suivant x est égale et opposée à la projection du poids suivant la direction x. De la même manière, la projection de T suivant Y est égale et opposée à la réaction du plan incliné suivant y (projection du poids suivant la perpendiculaire).

Attention aux projections (c'est soit cos ou sin de l'angle) !

[invite726932a4]

Il faut dessiner les vecteurs forces. La longueur des cotés des triangles correspond à l'intensité de force, l'angle entre les cotés représente l'angles entre les vecteurs.

[invite5c47911b]

Je crois que finalement j'ai su comment le resoudre, je vais poster la solution quand je termine!

[invite5c47911b]

1) P: Poids en Newton, Vertical Descendant d'intensite 3N
T: Tension du Ressort allant de A vers B
N: Reaction Du Support perpendiculaire a l'axe incline

2) Le Corps est un equilibre donc P+N+T=0 (Vecteurs)
-Px+0+Tx=0
-Psin(alpha)+Tcos(beta)=0
Tcos(beta)=Psin(beta)

T= (Psin(alpha)/cos(beta)=1.5/cos(beta)

3) a)Pour Beta=0
T=1.5/1=1.5

b)Pour Beta=30

T=1.5/cos30= approx. 1.73N

c)Pour Beta=60
T=1.5/0.5=3N

4) a) L=T/K=1.5/50=0.03m=3cm
b) L=1.73/50=0.0346m=3.46cm
c) L=3/50=0.06m=6cm

A+ Et Merci! (corrigez moi svp!)