Flux du champ magnétique à travers une surface fermée

[invite36795442]

Bonjour à tous,

Je m'intéresse en ce moment aux équations de Maxwell, mais je bloque sur celle qui exclut l'existence de monopoles magnétiques: div B=0.

En effet, je comprend bien que le flux du champ magnétique traversant une surface fermée soit nul lorsque la source du champ est à l'intérieur de cette surface fermée.
En revanche, je ne m'explique pas pourquoi le flux du champ magnétique est nul à travers une surface fermée lorsque la source est située hors de cette surface.

En fait, j'essaye tout bonnement de reproduire le raisonnement utilisé pour démontrer le théorème de Gauss: lorsqu'une charge est située à l'intérieur d'une surface fermée, son flux à travers cette surface est non nul et vaut q/E0 (avec E0 la permittivité du vide).
Et lorsqu'on considère la charge hors de la surface fermée, on voit que le flux du champ électrostatique est nul car la décroissance en 1/r² va être compensée par la croissance en r² de la surface.
On a donc le théorème de Gauss qui dit que le flux du champ électrostatique à travers une surface fermée est toujours proportionnel à la charge contenue dans cette surface.

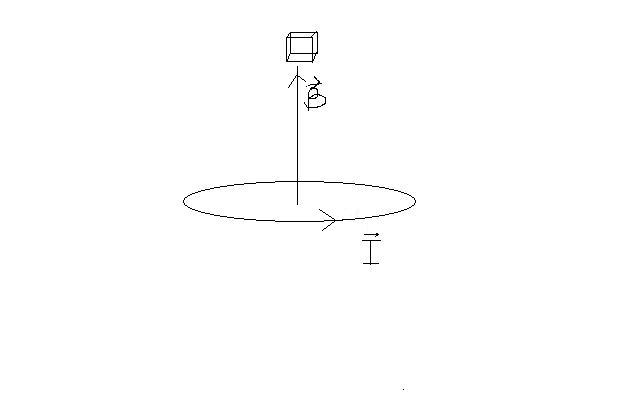
Hors, dans le cas du champ magnétique, et dans le cas particulier d'une spire, le champ selon l'axe de la spire varie en 1/r, je ne comprend donc pas pourquoi le flux de ce champ magnétique à travers une surface fermée ne contenant pas la spire serait nul.

Voila, merci d'avance pour vos explications.
-----

[LPFR]

Bonjour et bienvenu au forum.
Si vous voulez vous faire une image d'un champ vectoriel, je vous conseille plutôt celle du champ de vitesses d'une rivière. C'est plus concert qu'un champ électrique.

Prenez une surface fermés en grillage (fils infiniment fins) et mettez-la dans le courant. Vous voyez bien que le débit d'eau qui rentre dans le volume grillagé est le même que celui qui sort. Et ceci, indépendamment de la forme du grillage.
Mais ceci n'est vrai que si la divergence du champ est nulle, comme c'est le cas pour la vitesse de l'eau dans une rivière.
Je pense que vous trouverez intéressant ce petit fascicule sur la signification physique du gradient, divergence, rotationnel, etc.:
http://forums.futura-sciences.com/at...aire-nabla.pdf

Pour ce qui est de l'inexistence des monopôles magnétiques qui ont comme conséquence div B = 0, c'est une constatation expérimentale. Pas une nécessité théorique. De centaines de chercheurs on cherché pendant des décennies les monopôles (peut-être qui y en a qui cherchent encore) et ils n'ont rien trouvé.
Si un jour on venait à en découvrir, il suffirait de modifier l'équation de Maxwell et l'écrivant div B = µ_oρ_m
Et continuer le cours en disant:
"...comme ces monopôles sont rares, on perd très peu de généralité en nous limitant au cas où il n'y a pas de monopôles dans le coin et on écrit donc div B = 0".
Au revoir.

[invite36795442]

Tout d'abord, merci de votre réponse.

J'avais déjà lu ce formulaire sur l'opérateur nabla, je le trouve effectivement très bien fait.


J'ai bien saisi que la divergence du champ magnétique était nulle, le fait qu'en tout point, autant de champ arrive qu'il en sort, ce qui traduit l'inexistence (à priori) des charges magnétiques.

Mon souci réside dans la manière de le montrer, j'essaye de distinguer deux cas possibles (comme j'ai fait pour le théorème de Gauss, et donc pour la divergence du champ électrostatique):
Le cas où la source du champ est dans la surface de Gauss,
et le cas où la source est hors du champ.

Pour illustrer mon problème, voila un petit dessin:




Le champ B est produit par une spire portant un courant I.
Grace à l'étude des symétries et des invariances de la distribution de courant, on comprend que le champ B en tout point de l'axe de la spire est dirigé selon cet axe, et sa norme varie en 1/r.
Ma question est: comment dans ces conditions montrer que le flux du champ magnétique à travers la surface fermée dessinée est nul?

Merci d'avance.

[LPFR]

Re.
Dans ce cas d'espèces le seul moyen pratique est utiliser le théorème de Gauss. Car calculer le flux à travers les surfaces du cube "à la dure" c'est une galère. Ce serait légèrement moins horrible si à la place du cube vous aviez un cylindre. Mais c'est quand même une galère. Car il faut calculer les composantes de B dans tout l'espace pour calculer le produit scalaire B.dS dans chaque point de la surface et intégrer.
Non; franchement il faut être vraiment motivé.

Votre phrase: "Le cas où la source du champ est dans la surface de Gauss," m'inquiète.
Il n'y a pas de source du champ. les lignes de force sont toutes fermées (div B = 0).

Je crois que je n'ai pas compris ce que vous voulez faire.
A+

[A voir en vidéo sur Futura]