Electrotechnique de puissance: exercice

[invite698b14a9]

Bonjour,

Je ne sais pas si je poste dans le bon forum, je vous laisse le soin de déplacer ce sujet si besoin est.

Voilà, j'ai cet exercice à faire:

Exercice 5 :
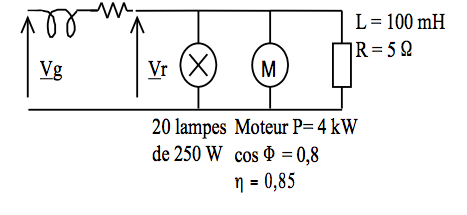
Soit une ligne monophasée 50 Hz distribuant de l'énergie à un atelier composé de lampes à incandescence, d'un moteur alternatif et d'un électroaimant (bobine constituée d'une inductance dont la résistance ne peut être négligée – on utilisera un schéma équivalent série).
Les caractéristiques de la ligne monophasée sont Vr = 230 V, r = 0,3 Ω et l = 4 mH.



Précisions: Lampes=Resistances / Puissance mécanique moteur=4 kW / Moteur=Inductif.

a) Calculer le module du courant de ligne par la méthode de Boucherot appliquée à l'atelier. En déduire la section
approximative de la ligne en cuivre nécessaire pour véhiculer ce courant (δmax= 5 A/mm2).
b) Déterminer le facteur de puissance de l'ensemble de l'atelier.
c) Montrer qu’en ajoutant un condensateur à l’entrée de l’usine, on peut ramener ce facteur de puissance à 1 et calculer la
valeur du condensateur à insérer.
d) Calculer le module et l'argument de Vg et les pertes induites dans la ligne et la puissance apparente de la source dans les
deux cas suivants:
- sans compensation
- avec compensation

____
Nous avons faits une correction de cet exercice mais je n'ai pas tout compris.
Pour moi,
Lampe=Resistif: S=P et Q=0
Moteur=Inductif: P=0 et S=Q

Est-ce exact?
Puisque dans la correction, nous avons pris en compte une puissance active pour le moteur, or P=0 non ?

Merci d'avance pour vos réponses,

Bonne journée à vous,
-----

[phys4]

Bonjour,
Vous donnez une correction très incomplète :
La correction devrait comprendre le calcul de l'impédance de l'électroaimant à 50 Hz et son courant avec son déphasage.
La puissance utile du moteur permet de calculer le courant puisque le rendement et le déphasage sont donnés.
Pour les lampes le calcul du courant est très facile.

Le calcul des pertes dans la ligne se fait à partir du courant total. Avez vous compris ce que signifie avec et sans compensation ?

Pouvez vous donner plus de détails sur votre correction ?

[invite698b14a9]

En fait, les propositions que j'ai donné étaient de mon point de vue, je voulais savoir si cela était exact?
La correction a été faite en donnant simplement les résultats:

a) Pt=20*250 + 4000/rendement + (230^2*cos(Phase elec))/Module(Z)
où z=R+jlw

J'ai déjà des problèmes ici pour la puissance active du moteur: Pour moi, si il est purement inductif, il n'a pas de puissance active non ? Sa puissance est essentiellement réactive?

Qt=5,67 KVar
St=11,22 KVA
Iligne=48,8 A
S>=9,75 mm^2

b ) fp=Pt/St=89%

c) c=311.10^-6 F

Je voudrais déjà essayer de répondre à ces trois premières questions avec vous, merci d'avance et bonne soirée.

[stefjm]

Bonsoir,
Un moteur n'est pas inductif pur sinon ce n'est plus un moteur.
P et Q sont tous les deux positifs pour un moteur globalement inductif. (et résistif aussi)

[A voir en vidéo sur Futura]

[invite698b14a9]

C'est vrai...
Donc, au calcul de la puissance active totale, je fais:

Pt=20*250 + 4000/rendement + (230^2*cos(Phase elec))/Module(Z)

où - Rendement=0,85
- Phase elec=Arctan(Lw/R) (diagramme de Fresnel) : D'où cos(phase elec)=cos(Arctan(Lw/R)
- Module(Z)=(R^2+L^2*w^2)^1/2 .

Je trouve: Pt=9967,3 W

Est-ce exact?

[phys4]

Puissance exacte.

Je suis d'accord aussi avec le corrigé, pour le courant total et la capacité de compensation. Allez vous y arriver ?

[invite698b14a9]

Alors:

a) Pour la puissance réactive:

Je fais Q(moteur)=P(moteur)*tan(arcos( 0,8)
AN: Q(moteur)=3529,4 VAR

Je fais Q(L,R)=P(L,R)*tan(Phase elec)
Or Phase elec=Arctan(Lw/R) : D'où Q(L,R)=P(L,R)*(Lw/R)
AN: Q(L,R)=1662,7 VAR

Qt=5,192 kVAR (Erreur?)

Pour la puissance apparente:

S=(Pt^2+Qt^2)^1/2
S=11,24 kVA

Pour le courant de ligne :

S=U.I
I=S/U (U=230V)
I=48,9 A

b) Pour le facteur de puissance:

f=Pt/S
f=89%

Pour la section approximative de la ligne de cuivre:

Je ne vois pas .

c) Pour ramener le facteur de puissance à 1 avec un condensateur, on sait qu'un condensateur est purement réactif, ce qui signifie que la puissance active totale ne changera pas. Il faudra donc faire baisser la puissance apparente à environ 9967 W. D'où une différence de 1273 VA.

Ainsi S(condensateur)=-1273 VA=-U^2*C*w
D'où: C=S/(U^2*w)

AN: C=-1273/(230^2*2*Pi*50)=76*10^-6 F (Erreur? )


Merci d'avance pour vos réponses,

Bonne journée.

[phys4]

Alors:

a) Pour la puissance réactive:

Je fais Q(moteur)=P(moteur)*tan(arcos( 0,8)
AN: Q(moteur)=3529,4 VAR

Je fais Q(L,R)=P(L,R)*tan(Phase elec)
Or Phase elec=Arctan(Lw/R) : D'où Q(L,R)=P(L,R)*(Lw/R)
AN: Q(L,R)=1662,7 VAR

Qt=5,192 kVAR (Erreur?)

Pour le moteur nous n'avons pas la résistance, c'est seulement la puissance électrique fournie (4000/rendement) qui nous donne la puissance active. Pour le facteur de puissance nous avons la phase, donc R et L sont inconnus. Vous ne pouvez pas vérifier directement.
Les 3529.4 VAR sont corrects. Les autres valeurs ne correspondent à rien.
Pour le circuit R,L j'ai 261.28 Watts et 1641.97 VAR

S=U.I
I=S/U (U=230V)
I=48,9 A

b) Pour le facteur de puissance:

f=Pt/S
f=89%

Pour la section approximative de la ligne de cuivre:

La formule est donnée pour la section de la ligne, il suffit de l'appliquer au courant total S = I /5 mm2 ce qui fait environ 10 mm2

c) Pour ramener le facteur de puissance à 1 avec un condensateur, on sait qu'un condensateur est purement réactif, ce qui signifie que la puissance active totale ne changera pas. Il faudra donc faire baisser la puissance apparente à environ 9967 W. D'où une différence de 1273 VA.

Ainsi S(condensateur)=-1273 VA=-U^2*C*w
D'où: C=S/(U^2*w)

AN: C=-1273/(230^2*2*Pi*50)=76*10^-6 F (Erreur? )

Le condensateur a bien une puissance réactive négative. Il faut simplement faire puissance réactive = - puissance réactive du condensateur et faire le calcul avec la puissance réactive totale 5171.3 VAR,

dans le circuit les puissances actives et les puissances réactives s'ajoutent séparément, il ne faut les combiner que pour trouver le courant total et le facteur de puissance.

Bonne journée.

[invite698b14a9]

"Pour le circuit R,L j'ai 261.28 Watts et 1641.97 VAR"

Moi je ne trouve pas exactement cela, pour moi:

P(R,L)=(230^2*cos(arctan((0,1* 2*Pi*50)/5)))/RACINE(5^2 + (0,1*2*Pi*50)^2)
P(R,L)=261,37 Watts

Q(R,L)=(230^2*sin(arctan((0,1* 2*Pi*50)/5)))/RACINE(5^2 + (0,1*2*Pi*50)^2)
Q(R,L)=1642,26 VAR

Où je fais la faute ?

Merci d'avance.

[phys4]

C'est correct, j'avais fait un arrondi à la troisième décimale sur une valeur intermédiaire.

[invite698b14a9]

Très bien .

Alors, aisément, j'ai:

Pt=9967,3 W
Qt=5171,66 VAR
St=11229,12002 VA
fp=Pt/St=88,76 %
I=48,8 A

Pour la section, je ne connais pas la formule

Et pour le condensateur:
J'ai compris: le but est de supprimer la puissance réactive totale pour n'obtenir que de la puissance active et apparente, et Pt=St, d'où fp=1.
Mais mon calcul semble incohérent avec la correction: Qt(5171,66 VAR)-U^2*C*w=0 Je trouve C=311,2.10^-6 F ?

Merci d'avance,
je vous souhaite une bonne fin de journée.