Bonjour,
Après avoir recherché sur le forum des discussions similaires, je n'ai toujours pas trouvé la réponse souhaitée.
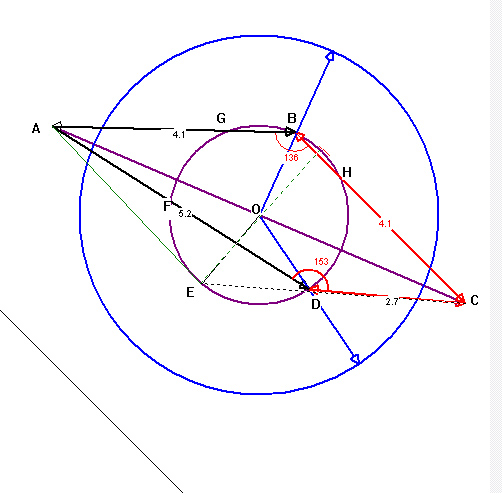
Je dois programmer un petit jeu de billard sous java mais pour cela j'ai besoin de modéliser le choc entre deux boules.
Deux cas :
Le premier:Une boule en mouvement percute celle qui est immobile.
Le second :deux sont en mouvement.
J'ai besoin de connaitre la nouvelle trajectoire ainsi que la nouvelle vitesse de chacune d'entre elle.
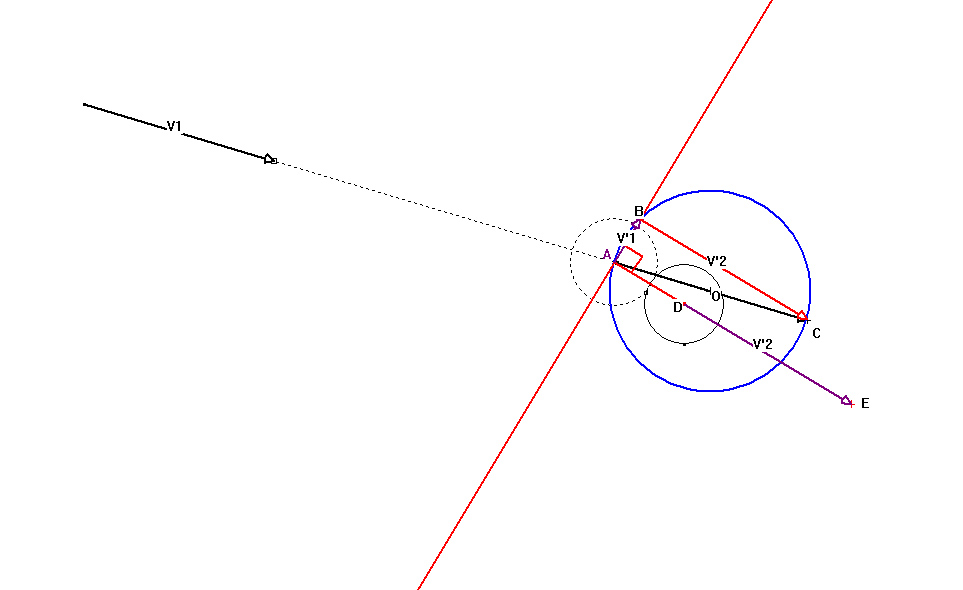
Pour le premier cas, j'ai reussi à obtenir la nouvelle vitesse de chacune des boules et la trajectoire suivi par la boule initialement immobiles. Toutefois je n'arrive pas à obtenir la nouvelle trajectoire de la boule qui était en mouvement.
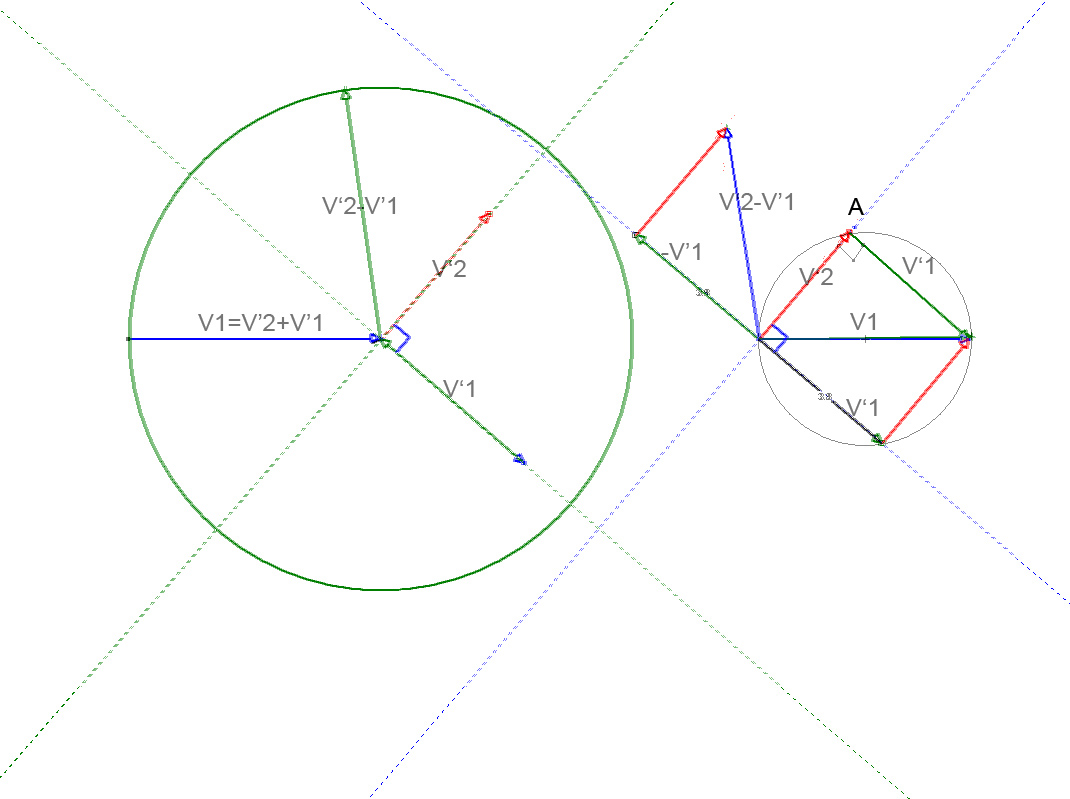
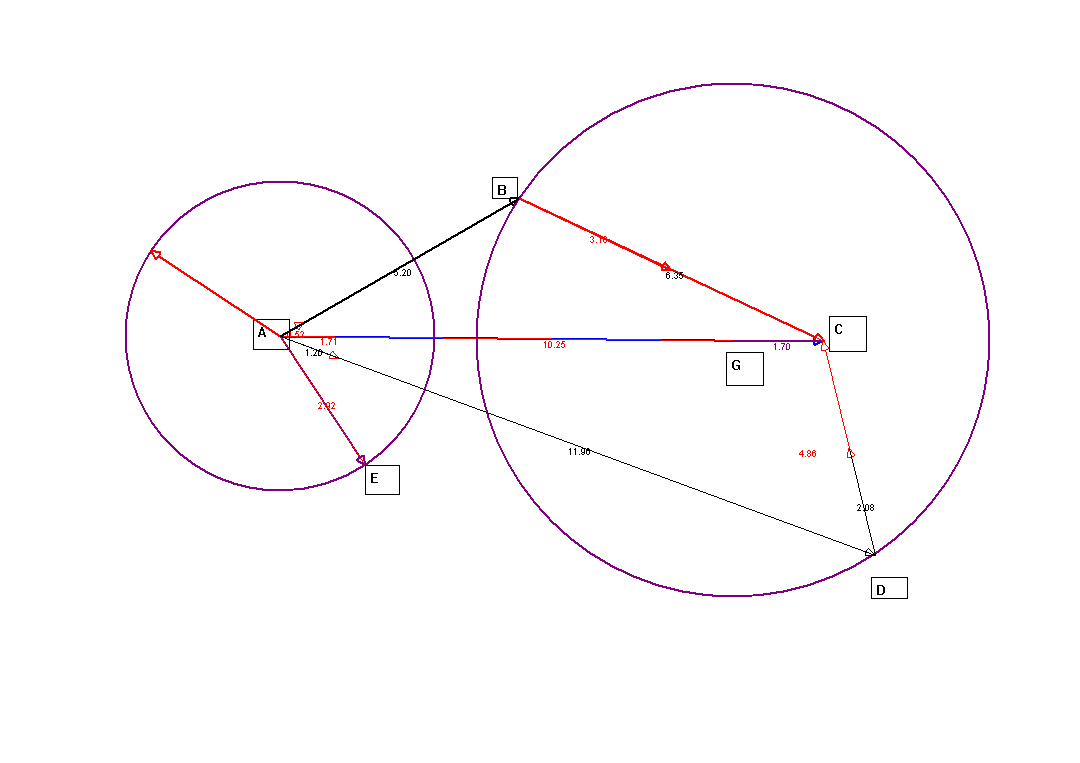
Pour ce qui est du deuxième cas, j'ai essayé avec la même méthode ( quantité de mouvement) et je suis un peu bloqué...
Je caractérise la boule par une vitesse et un angle (celui entre l'axe des abscisses et celui de sa direction).
Si quelqu'un a un idée des nouvelles trajectoires ( angle et vitesse) ?
-----