Choc élastique avec des billes

[elbart]

Bonjours,

J'ai cherché un peu sur le net les formules de physique qui interagissent quand survient un choc entre deux objets. J'ai trouvée qu'il existait les choc élastiques et qu'avec cette formule :



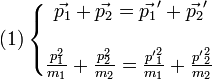
(tiré de wikipedia) je pouvais obtenir mes vecteurs vitesses mais seulement dans le cas ou les vecteurs vitesses des deux billes étaient colinéaire à la droite passant par leur centre (de ce que j'ai compris).

Comment puis-je calculer les vecteurs vitesses si les deux billes rentre en collision en se frôlant a peine, enfin du moins pas face à face, car cette formule (j'ai tester en simulation) ne fonctionne pas dans ces cas.

Merci de votre aide.
-----

[LPFR]

Bonjour.
Il faut déménager dans le repère du centre de masses. Lequel, dans ce repère, ne bouge pas.
Faites un dessin.
Suivant le paramètre de la collision (la distance entre les droites décrites par les centres de billes) le contact entre les billes se fait sur un plan plus ou moins incliné. Ce plan est perpendiculaire à la droite qui relie les deux centres au moment du contact. Les billes se réfléchissent "spéculairement" sur ce plan et repartent avec la même vitesse (en module) que celle d'arrivée.
Une fois les nouvelles vitesses calculées il faut déménager sur le repère d'origine.
Au revoir.

[elbart]

Oula, c'est très intéressant mais je n'ai pas tout compris ^^, je ne suis qu'en première S.
Donc il faut que je trouve le centre de masse de ma bille (donc le milieux) et que je fasse un repère à partir de ce point. La suite je ne comprend pas vraiment...
J'ai oublié de préciser que mon repère est en 2D donc je comprend pas vraiment "le contact entre les bille se fait sur un plan plus ou moins incliné."
Ensuite j'ai compris que le plan était perpendiculaire a la droite qui relie les centres. Par contre le fait que les billes se réfléchissent "séculairement" la je ne comprend absolument pas.

Merci.

[Amanuensis]

Si les billes sont de masse égale, imaginez qu'elles vont à des vitesses exactement opposées, mais pas nécessairement sur une même ligne. Et étudiez ce qui se passe dans ce cas là : les billes vont se toucher mais pas nécessairement au centre. Il apparaît alors une droite tangente au deux billes, et passant par le point de contact. Cette droite (un plan en 3D) qui va faire office de "miroir" lors du choc (spéculaire = miroir, je pense que mot voulu était "spéculairement" et non "séculairement"), chaque bille rebondit sur cette droite comme un rayon lumineux sur un miroir.

Si vous avez compris ce cas particulier, l'étape suivante est de comprendre qu'on peut toujours se ramener à ce cas particulier par un changement de repère particulier.

[A voir en vidéo sur Futura]

[invite490b7332]

Si les billes sont de masse égale, imaginez qu'elles vont à des vitesses exactement opposées, mais pas nécessairement sur une même ligne. Et étudiez ce qui se passe dans ce cas là : les billes vont se toucher mais pas nécessairement au centre. Il apparaît alors une droite tangente au deux billes, et passant par le point de contact. Cette droite (un plan en 3D) qui va faire office de "miroir" lors du choc (spéculaire = miroir, je pense que mot voulu était "spéculairement" et non "séculairement"), chaque bille rebondit sur cette droite comme un rayon lumineux sur un miroir.

L'image d'un miroir fictif est particulièrement explicite. Très parlant. Je me demandais s'il était possible d'avoir la même démarche pour représenter le chaos moléculaire, à savoir h(v1,v2)=f(v1)*g(v2).
Peut-on imaginer un système qui décorrèle les vitesses après le choc ??

[elbart]

Je comprend le principe du miroir pour des vitesses opposées mais je n'arrive pas à comprendre comment je peut changer le repère dans un cas ou les billes ont des vitesses et des masses différentes... Est-il possible de faire une petit exemple ?

[Amanuensis]

Je comprend le principe du miroir pour des vitesses opposées mais je n'arrive pas à comprendre comment je peut changer le repère dans un cas ou les billes ont des vitesses et des masses différentes... Est-il possible de faire une petit exemple ?

En mécanique classique, ajouter une même vitesse à toutes les vitesses est un changement de repère.

Dans le cas d'un choc, on le "symétrise" en ajoutant (changement de repère donc) la vitesse v qui annule .

Dans le cas de masses égales, on obtient , les nouvelles vitesses sont et , donc bien exactement opposée l'une de l'autre.

[LPFR]

Bonjour.
C'est peut-être plus simple à comprendre en calculant la vitesse du centre de masses:



Pour passer dans le repère du centre de masses on soustrait cette vitesse de deux autres.
Pour revenir au repère originel, on ajoute cette vitesse aux autres.
Au revoir.

[invite490b7332]

Si l'addition d'une vitesse correspond à un changement de repère, la multiplication correspondrait-elle à une augmentation de la dimension (2D à 3D par exemple)?

[LPFR]

Re.
Je ne vois pas de signification physique à la multiplication de deux vitesses.
(En dehors du calcul de l'énergie cinétique).
A+

[triall]

Bonjour, Elbart .
Suite à un ancien post, il me semble qu'il faut comprendre que si l'on ne tient pas compte du point de contact (une boule peut frôler l'autre , ou la prendre en plein centre , le rebond ne sera pas pareil) on aura un ensemble de solutions .
Voila un ensemble de solutions pour des masses égales.(on ne tient pas compte du point de contact)
CHOC-M-M.jpg
vec(AB) représente vec(m.V1) , vec(BC)=vec(mV2) ; l'ensemble des solutions se trouve sur le cercle de centre 0 milieu de AC .(Points D) , car on a , par construction vec(m.V1) +vec(m.V2) =vec(m.V1') +vec(m.V2')=vec(AC) ; et 1/2 mV1²+1/2mv2²=1/2mv1'²+1/2mV2'² soit AB²+BC²=AD²+BD² A démontrer ci dessous .
Voila la démonstration :L'astuce de la démo, c'est de savoir que dans un choc élastique, la norme de (vec(AB)-vec(BC)) est constante , elle est égale à Norme (2vec(OB) ) ici, c'en est aussi la démonstration . C'est la vitesse relative des 2 boules.
On s'occupe de chercher vec(AB)-vec(BC)=vec(AB)+vec(CB)=vec(AO )+vec(OB) +vec(CO)+vec(OB) (c'est l'astuce de la démo )
or, vec (AO)=-vec(CO) , on a alors vec(AB)-vec(BC)=2vec(OB)
ce qui donne AB²+CB²-2vec(AB).vec(BC)=4OB² (1)
Ensuite de vec(AB)+vec(BC)=vec(AC) on a AB²+BC²+2vec(AB).vec(BC)=AC²(2 )
En combinant (1) et (2) on obtient AB²+BC²=2OB²+AC²/2
On voit donc que si OB² est constant , (B se promène sur le cercle) AB²+BC² est aussi constant car Ac² étant constant par définition .
On a alors bien entendu AD²+DC²=2OB²+AC²/2=AB²+BC²
Le cercle de centre O est donc bien l'ensemble des solutions pour les rebonds avec masse égale.

Pour ce qui est de masses différentes, m1 et m2 ; c'est la même solution mais au lieu de prendre O milieu de AC, on prend G centre de gravité de AC avec GA/GB=m1/m2
choc-m1-m2.jpg
Je n'ai pas la démonstration, mais elle doit être du même genre que ci dessus .
Ici un exemple numérique avec m1=10 ;m2=2 : V1=0.5197 ; V2=3.176 .Vous pourrez vérifier qu'ici m1V1²+ m2V2²=10.(0.5197)²+2.(3.176²)= 10.(1.001)²+2.(2.535²) .
A noter, le petit cercle de gauche est norme (vecV1-VecV2) qui est constante , car quand je fais varier D sur le cercle de centre G, ... E construit tel que vec(AE)= vec(V1)-Vec (V2) dans la figure , donc E reste sur le cercle de centre A de norme norme(vec(V1)-Vec (V2) ).
Pour un choc élastique, donc , même avec des masses différentes, la vitesse relative est conservée avant et après le choc !

La suite serait de tenir compte du point de contact et on aurait alors une solution unique, appartenant à ces ensembles de solutions .
Il semble qu'il y ait une solution particulière, obtenue en prenant D le symétrique de B par rapport à G (D sur le cercle évidement) qui doit correspondre à un choc "frontal" .

[elbart]

Bon, je crois que j'ai compris grâce aux réponse de LPFR et Amanuensis,

Je pose la formule Amanuensis : On Obtient Donc la vitesse du centre des masses donnée par LPFR. Ensuite j'ajoute cette vitesse à toutes les autres vitesse pour obtenir les nouvelles vitesses d’après ce que j'ai compris.

L'exemple ci=dessous est-il par conséquent juste ? :

Donc :
Par conséquence les nouvelles vitesses sont :
et

Mais quand je regarde ce que sa donne sur papier... Sa me semble étrange tout de même.
Est-ce juste ?

[Amanuensis]

Il y a un problème de signe.

La vitesse du centre de masse n'est pas celle qu'il faut ajouter, mais celle qu'il faut soustraire.

[LPFR]

...Ensuite j'ajoute cette vitesse à toutes les autres vitesse pour obtenir les nouvelles vitesses d’après ce que j'ai compris.
...

Bonjour.
Non. Il faut soustraire la vitesse du centre de masses aux autres.
Pour vous souvenir, cela permet que la nouvelle vitesse du centre de masses soit nulle.
Au revoir.

[elbart]

En lisant le post d'Amanuensis j'avais compris qu'il fallait ajouter ^^. Erreur de ma part, donc nous avons :

et

Donc effectivement sur le papier sa rend mieux mais sa dépend du point d'impact, mais rajouter ce paramètre complique beaucoup les équation non ?
Si ce n'est pas hors de porté quelqu'un pourrait-il m'expliquer comment prendre en compte le point d'impact ?

[LPFR]

Re.
Faites un dessin et regardez les vitesses que vous avez dans le nouveau repère: elles sont parallèles. Tracez les droites que les billes parcourront. (La distance entre ces droites est le paramètre d'impact).
Au moment de l'impact, les deux centres se trouveront à une distance de (R1+R2) l'un de l'autre.
Maintenant vous n'avez qu'un simple calcul de géométrie à faire pour trouver l'instant et la position de billes au moment du choc.
A+

[Amanuensis]

En lisant le post d'Amanuensis j'avais compris qu'il fallait ajouter ^^.

C'est bien ce que j'avais écrit. Quand vous avez résolu l'équation, vous vous êtes trompé de signe.

[elbart]

Re.

Mais LPFR ce que vous expliquer c'est pour retrouver le point d'impact à partir des vitesse, moi je cherche l'influence du point d'impact sur les vitesse car imaginons que la bille 1 frappe la bille 2 par dessus, les vecteur vitesse ne seront pas les même que si la bille 1 frappe la bille 2 par aux-dessus (du moins la direction voir uniquement le sens).

Ou alors je me trompe complètement ?

[LPFR]

Bonjour.
Je ne sais pas ce que vous entendez par "l'influence du point d'impact sur les vitesse".

Depuis le début de la discussion nous sommes en train de vous expliquer comment calculer les nouvelles vitesses et tenant compte des positions et vitesses de départ qui, elles, déterminent le point d'impact.
Au revoir.

[elbart]

Ha ok, donc depuis le début je comprend à l'envers moi ^^.
Pour moi depuis le début je cherche à calculer les nouvelles vitesses qui ont lieux après l'impact en tenant compte de la vitesse de départ, de la position et du point d'impact.