Bonjour,
-Voici une simulation d'un gaz soumis à le pression d'un piston. Ce gaz est représenté par des particules en mouvements, qui s'agitent, donnent une température au groupe de particules, et exerce une force sur le piston, résultant des multiples chocs élastiques que chacune des particules occasionnent sur le piston.
http://www.etomica.org/app/modules/s...applet_2d.html
-Dans un choc élastique idéal (comme le pendule de newton), lorsque on met en jeu trois billes identiques en masse, et que la première, ayant une vitesse initiale donnée, vient percuter les deux autres immobiles et voisines, selon la mécanique classique, la première bille A s'immobilise, la seconde B ne bouge pas, quant à la troisième C, elle se met en mouvement à la vitesse initiale de la première bille.
Peut-on penser qu'en fonction d'une masse particulièrement choisie du piston, les chocs multiples des billes du gaz excitées à l'intérieur du piston, puissent être vus comme une seule bille A heurtant le piston, considéré lui, comme la seconde bille B, et une grosse et unique particule derrière le piston jouant le rôle de ma bille C? Ainsi les particules du gaz multiples "donnent" leur vitesse à travers le piston (restant immobile) à une grosse et unique particule identique à la masse moyenne des particules du gaz qui viennent percuter le piston?
Merci d'avance.
-----



 par contact!
par contact!

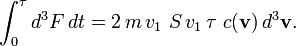
 ou
ou
 ?
? et
et 
 et à nouveau m disparaît. m qui est d'ailluers seulement la masse d'une molécule, alors que je veux la masse moyenne des particules venant frapper le piston. Je ne dois pas prendre le bonne piste?
et à nouveau m disparaît. m qui est d'ailluers seulement la masse d'une molécule, alors que je veux la masse moyenne des particules venant frapper le piston. Je ne dois pas prendre le bonne piste? Le Mmoy se cache dans mSC<v^2> je me dis en ayant tête F=ma, mais comment n'avoir que Mmoy en fonction de paramètre extérieur comme la température, la pression, le nombre de particule et sa masse propre...??? Dois-je ne plus que recourir à une simulation numérique pour avoir cette information basique? L'algèbre ne peut pas me donner une équation bien concise?
Le Mmoy se cache dans mSC<v^2> je me dis en ayant tête F=ma, mais comment n'avoir que Mmoy en fonction de paramètre extérieur comme la température, la pression, le nombre de particule et sa masse propre...??? Dois-je ne plus que recourir à une simulation numérique pour avoir cette information basique? L'algèbre ne peut pas me donner une équation bien concise?
 m étant la masse de la molécule. D'après les
m étant la masse de la molécule. D'après les 


