Bonjour tout le monde!
Voilà, je suis nouvelle ici et j'ai longuement hésité avant de venir vous demander de l'aide car je suis un peu coincée!
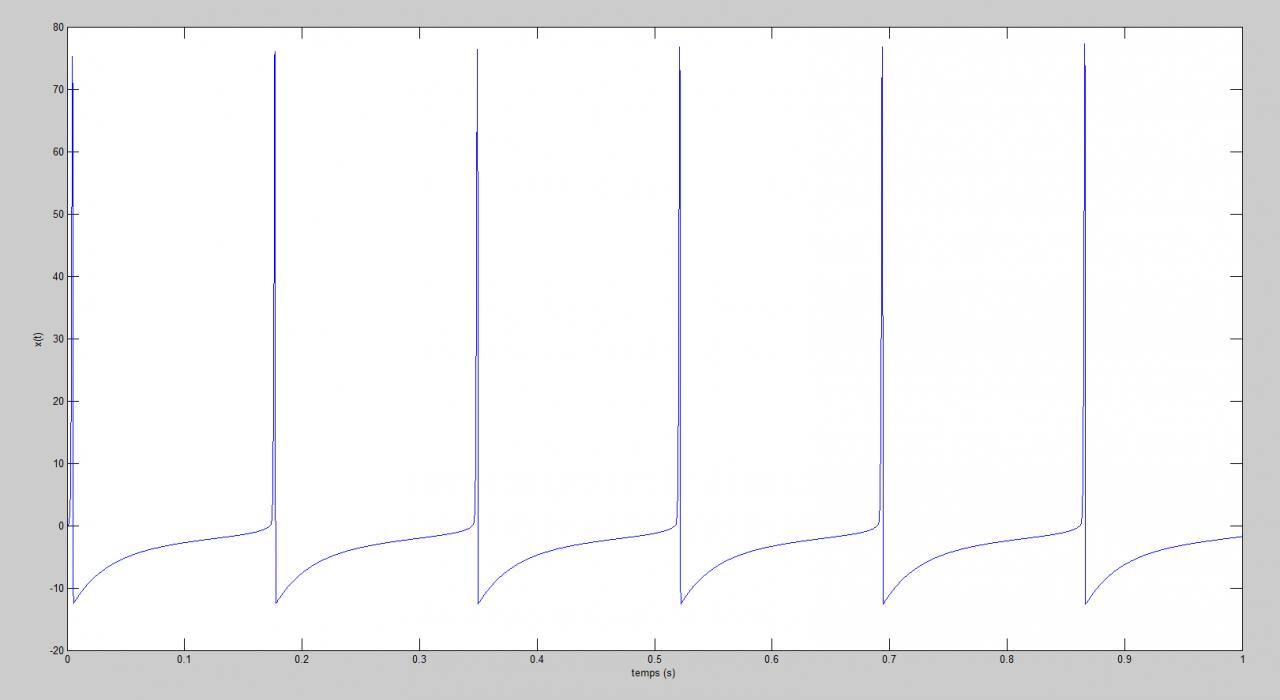
j'ai le schéma d'un signal x(t) généré par Matlab (il s'agit de la solution d'une équation différentielle) et je voudrais déterminer la période de ce signal toujours avec Matlab mais je n'arrive pas, plutôt je ne sais pas comment m'y prendre.
Le signal que j'ai est le suivant:
t=0:10^-4:1(s)
Merci d'avance.
Bjr àtoi et bienvenue sur FUTURA ,
Connais tu la DEFINITION de la période d'un signal ?
Peux tu donner la période d'un signal de 2 hertzs.
Reste à connaitre la forme de ton signal...on va attendre la validation.
Bonne soirée
Remoi,
Bon , Matlab ou as Matlab....c'est enfantin.
Te reste donc à connaitre la définition de la période d'un signal.
Au cas ou..:http://www.google.fr/url?sa=t&rct=j&...41248874,d.d2k
A+
Dernière modification par f6bes ; 21/01/2013 à 17h44.
Déjà merci pour votre réponse!
Pour votre question, la période Test: T=1/f, donc T=1/2=0.5s.
Pour reformuler ma demande, j'aimerai m'assurer que mon signal est périodique ou non sans me fier à la courbe (j'ai autres courbes à traiter à part celle que j'ai posté), c'est pour cela que j'ai pensé à calculer la période (en pensant que si le signal est non périodique, Matlab me renverra une erreur ou un message, enfin je ne sais pas).
J'espère que je suis un peu claire est que vous avez compris l'idée.
Remoi,
C'est QUOI la définition de ..périodicité d'un signal !
Ben si ton signal est NON périodique je vois pas COMMENT tu peux en déduire une ...période !
C'est...une ... évidence !
Faut tout de meme s'imprégner de ce que les MOTS veulent dire.
Tu peux à la RIGUEUR ...déterminer une période....MOYENNE qui risque fort d'etre...aléatoire.
A+
Dernière modification par f6bes ; 21/01/2013 à 18h17.
On a deux solutions :
la première, c'est que votre signal sera tout le temps le même, seule la periode changera. Dans ce cas un petit algo simple sera capable de le savoir.
Si vous voulez le savoir pour un signal quelconque, il faut passer par une FFT et là ça va devenir plus retors.
\o\ \o\ Dunning-Kruger encore vainqueur ! /o/ /o/
re...
j'aimerai savoir si Matlab peut déterminer si un signal numérique est périodique ou pas.
la définition de la période je la connais...
j'ai une demande précise, et je répète que mon signal est le résultat d'une équation différentielle (une série temporelle pour être plus précise), et j'ai beaucoup de signaux que je ne pourrai pas les vérifier visuellement un par un.
et à propos, je ne comprends pas ta façon de répondre à mon besoin.
en tout cas, merci à TOI.
Merci obi76 pour votre réponse.
Effectivement j'ai essayé d'utiliser la fonction FFT , j'ai vu quelques exemples en anglais mais sans pouvoir appliquer la fonction dans mon cas, il y a certainement un détail qui m'échappe.
Merci beaucoup.
J'ai fais un bout de scotch vite fait qui regarde l'écart de temps entre deux fois où le signal passe à la moyenne entre son maxi et son mini :
Si ça vous convient dites le nousCode:i = 0; j = 2; xmax = max(max(x(:,2))); xmin = min(min(x(:,2))); %normalisation du signal x(:,2) = (x(:,2) - xmin)./(xmax - xmin); while i < 2; %si le signal passe le seuil, on enregistre le temps if ((x(j,2) > 0.5) && (x(j-1,2) <= 0.5)) i = i+1; temp(i) = x(j,1); end j = j + 1; end %la periode est la différence entre les deux fois où le signal passe le seul (avec une dérivée positive, d'où la double condition dans le while) period = temp(2) - temp(1)
Dernière modification par obi76 ; 21/01/2013 à 18h47.
\o\ \o\ Dunning-Kruger encore vainqueur ! /o/ /o/
Bonjour,
Tu ne connais pas la definition de la periode et tu veux savoir si ton signal est periodique ????.....!!!
Je commencerai par rechercher la definition de la periode...si non cela sera difficile.
En science " Toute proposition est approximativement vraie " ( Pascal Engel)
Merci obi76 pour votre réponse, je suis entrain d'essayer de l'adapter à mon problème.
Pour les autres, je suis déçue par votre façon de parler, supposer que je connais pas de quoi je parle, comme si, au cas où j'étais ignorante, je n'aurais pas pu effectuer une recherche sur google, et vous recopier la réponse ici, sauf que je ne marche pas comme ça.
Bref, je vous tiens obi76 au courant de l'évolution de mon travail, et merci encore une fois.
Bonjour,
Tu calcule la FFT de ton signal (qui doit être périodique(enfin non)), la première composante est la valeur moyenne, la fréquence de la seconde (ou 1ere harmonique) est la fréquence de ton signal(enfin si).
Cordialement
Je vais mieux m'exprimer : si ton signal est périodique, la FFT va te donner un spectre discret aux fréquences 0, f0, 2f0, 3f0,... f0 étant la fréquence que tu cherches.
Merci beaucoup Thouxify pour ta réponse, c'est beaucoup plus claire pour moi maintenant.
La DFT ne donnera un spectre discret que dans de rares conditions (pas de bruit, pas de discontinuité aux extrémités et une histoire de multiple entier). En réalité tu obtiendras qqch dans ce style: http://www.mathworks.com/help/matlab/ref/new_fft2.gif
Après avoir éliminé la composante continue, tu peux chercher le maximum du module de la DFT et le comparer à la valeur moyenne: si l'écart est significatif (seuil à fixer), tu peux en déduire que ce max correspond à une fréquence fondamentale, qu'il y a quelque chose de périodique dans ton signal. Avant de faire fft(), tu peux multiplier ton signal par une fenêtre de Hamming pour de meilleurs résultats.
Dernière modification par Bruno ; 21/01/2013 à 22h46.
Et ce n'est pas son cas?Envoyé par Bruno
Si son signal était bruité, or il ne l'est pas. Dans son cas, la troncation entrainerait juste un élargissement des fréquences (si je me souviens bien la convolution de la FFT de la fenêtre sur le spectre à étudier)tu peux multiplier ton signal par une fenêtre de Hamming pour de meilleurs résultats.
D'ailleurs je me demande si on peut considérer que le fait que le résultat donné par matlab n'est pas infini est équivalent à une troncation par une fenêtre de la taille de la matrice? Dans ce cas pourquoi le spectre d'un sinus donné par matlab est un dirac, et pas un sinc?
a+
Dans l'exemple, on voit bien une discontinuité sur les bords et la taille de la fenêtre n'est pas vraiment un multiple entier de la période. Une bête discontinuité ajoute des merdes incroyables dans la DFT.
Oui c'est ça, cela dit le but n'est pas d'avoir la meilleure résolution fréquentielle possible mais d'avoir un pic pas trop noyé dans les lobes secondaires de la fenêtre. De ce point de vue, n'importe quelle fenêtre fait mieux que la rectangulaire.Si son signal était bruité, or il ne l'est pas. Dans son cas, la troncation entrainerait juste un élargissement des fréquences (si je me souviens bien la convolution de la FFT de la fenêtre sur le spectre à étudier)
Fais l'essais sous Matlab, tu auras bien un sinc décalé par le dirac du sinus.
A oui tu as raison! En plus si latimoon13 veut mesurer des périodes différentes, rien ne dit qu'elle aura toujours un multiple de périodes à chaque fois! Désolé^^
a+
Bonsoir à tous,
comme Bruno le suggère, une FFT ne sera équivalente à une DSF que si le signal analysé l'est sur un multiple entier d'une période. Ce qui suppose donc à la base que le signal est périodique, ce que veut vérifier Latimoon13 ; on tourne en rond !
Si un signal est périodique et non sinusoïdal, alors son spectre est harmonique. Il faut donc vérifier l'harmonicité du spectre, par exemple en faisant un cepstre et en prenant la première quéfrence (non, il n'y a pas de faute de frappe). Cela fonctionne même si on fait ce traitement sur un nombre de périodes non entier. Et pour minimiser les effets de bord et améliorer la résolution : fenêtrage et "zero padding".
J'aurais du préciser que tu obtiendrais ton sinc décalé en faisant du zero-padding assez important. Ne jamais oublier que la FFT est un algorithme rapide pour calculer une DFT, et qu'une DFT n'est rien d'autre que le calcul des coefficients de Fourier pour un signal discret périodique. Cela signifie que le fenêtrage par rectangle ne sert à rien, car la DFT "périodise" de toute façon ton signal fenêtré de -infini à +infini avant d'en calculer la transformée de Fourier sur une période. D'où l'intérêt de faire du zero-padding: plus on ajoute de zéros, plus l'espace entre les copies du signal est important, et plus on tend vers la transformée de Fourier du signal non-périodique.A oui tu as raison! En plus si latimoon13 veut mesurer des périodes différentes, rien ne dit qu'elle aura toujours un multiple de périodes à chaque fois! Désolé
a+
Bonsoir,
Non, justement la fenêtre rectangulaire sert à définir cette période. L'algorithme ne la trouve pas tout seul.
Du zero padding en temporel est équivalent à une interpolation en fréquentiel. On affine, mais on ne se rapproche pas d'une transformée de Fourier. Pour faire cela, il faut augmenter la période d'analyse.
Je sais bien que la taille de la fenêtre sert à définir la période et la résolution fréquentielle, ce que je voulais dire c'est que fft(y(k)) ne donne pas la DFT de y(k) mais bien de y(k) périodisé, contrairement à ce que l'usage laisse entendre et qui est source de confusion style "pourquoi la DFT de rect*sin n'est pas un sinc ?". Pour la transformée de Fourier du signal non-périodique, je parlais du signal fenêtré, ici rect*sin(wt). Le zéro-padding sert donc bien à se rapprocher de la véritable transformée de y(k), et pas de y(k) périodisé.
Dernière modification par Bruno ; 24/01/2013 à 00h46.
Bonsoir,
Ce qui est la même chose : impossible d'avoir un enregistrement d'un signal entre -infini et +infini... Une DFT ne s'entend que sur un signal tronqué, tout autre calcul est irréalisable.
Ca n'en est de toutes façons pas un.
Je pense que tout ceci n'est pas clair : si le signal est fenêtré en fenêtre rectangulaire, alors il est forcément périodisé par le fenêtrage.
Je crois que ce que tu veux dire, c'est qu'il est faux de comparer la DFT d'un signal tronqué par une fenêtre rectangulaire avec la transformée de Fourier d'un signal multiplié par la fonction porte. Pour moi, une fenêtre rectangulaire n'est pas une fonction porte.
Quant au zero padding sur une DFT permettant de se rapprocher d'une transformée de Fourier d'un signal multiplié par une fonction porte, on retombe sur ce que j'ai dit plus haut, à savoir qu'une DFT se rapproche d'une transformée de Fourier si l'on augmente la période d'analyse. Donc ton exemple n'est valable que parce que ce que tu appelles "signal non périodique" est composé de zéros en dehors de la partie analysée. Faire du zero padding revient donc à augmenter la période d'analyse... Essaye avec n'importe quel autre signal moins remarquable, tu verras que ce que tu avances ne fonctionne pas.
Dernière modification par phuphus ; 24/01/2013 à 21h59.
Non, le fenêtrage ne périodise rien du tout, il ne fait que produire une fonction à support fini. La "périodisation" est intrinsèque à la DFT parce que la DFT, comme les séries de Fourier, suppose un signal périodique.
Si tu appelles fonction porte la fonction nulle partout et unitaire sur [-T/2;T/2], c'est strictement la même chose.
Elle se rapproche de la TF du signal original non tronqué, mais en aucun cas de la TF du signal tronqué non-périodique.
Faire du zéro-padding revient à contourner la périodisation forcée par la DFT, donc à se rapprocher vers la TF du signal tronqué non-périodique.
Dernière modification par Bruno ; 24/01/2013 à 22h23.
