Calcul debit moyen
Bonjour,
Voici mon problème:
Dans un exercice on me demande de calculer le debit massique moyen, voici les parametres :
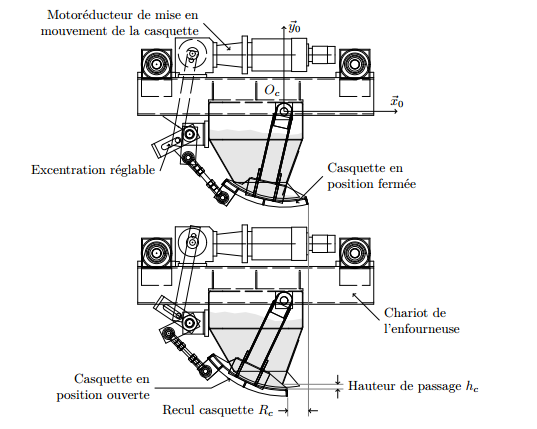
L’ouverture de la casquette du distributeur est un rectangle de longueur Lc = 2200 mm (égale à la
largeur du four) et de hauteur hc pouvant être réglée manuellement de 5 à 75 mm (voir figure 6). La fréquence
d’ouverture de la casquette, fc est réglable par asservissement de 0,083 Hz à 0,25 Hz. La vitesse d’avance du
chariot vc est réglable par asservissement de 8,3 × 10−3 m · s−1à 8,3 × 10−2 m · s−1. L’amplitude du recul Rc
de l’extrémité de la casquette est réglable manuellement de 30 à 80 mm.
On accepte que (voir figure 6), lors de l’ouverture de la casquette, une quantité de poudre tombe à la surface
du four et qu’ensuite, lors de la fermeture, la même quantité se retrouve, par gravité, au dessus de la casquette
lorsque celle-ci est refermée. On effectue, dans un premier temps, un calcul théorique ne prenant pas en compte
les propriétés réelles d’écoulement de la poudre de verre. Le volume de poudre qui tombe à la surface du four à
chaque aller retour de la casquette est donc assimilé à un volume parallélépipédique de valeur hc × Lc × Rc.
Comment faire pour trouver le trouver ? J'ai la formule Dm=dV*masse volumique et dV=volume/temps mais je ne voit pas comment faire intervenir vc.
Merci d'avance de votre réponse.
-----
Envoyé par js95690 
