Collision 2D entre une masse et une ligne rattachée à deux autres masses.

[Petipo]

Bonjour,
je créé actuellement un petit programme dans lequel je dois simuler la collision 2D entre une masse et une ligne rattachée à deux masses.

Il s'agit donc d'un problème de physique. Mes connaissances en ce domaine étant ma foi plutôt restreintes, et après avoir cherché un bon moment sur divers site pour ne finalement trouver que des explications mécaniques trop générales pour que j'arrive à m'en débrouiller ou trop spécifiques (collision d'une balle contre un mur, de deux balles, en général pour les jeux vidéos), je sollicite votre aide.

Le problème :


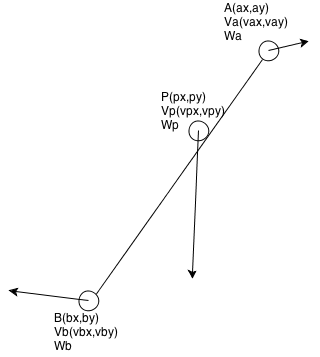
Un point P(x,y) de masse Wp rentre en collision avec une ligne reliant deux autres points A et B de masses Wa et Wb. La "ligne" n'a pas de masse, ne peut pas se plier et est extensible (selon son propre axe) à volonté. Les trois points P, A et B possèdent tous trois une vitesse qui leur est propre : Vp, Va et Vb respectivement. Les coordonnées du point d'impact sont parfaitement connues puisqu'il s'agit, lors de la collision, des coordonnées du point P.
Ainsi, tout mon problème réside dans le calcul des nouvelles vitesses pour ces 3 points, puisque j'imagine qu'elles vont toutes être modifiées en fonction de divers paramètres (leurs positions - et donc l'inclinaison de la ligne -, leurs masses et leurs vitesses au moment de l'impact).

Un petit schéma pour résumer le tout :


Voilà. N'importe qu'elle aide, piste, réponse partielle ou complète sera la bienvenue.
-----

[LPFR]

Bonjour et bienvenu au forum.
Ce qui se conserve dans ce type de choc est le moment linéaire (quantité de mouvement du système) d'une part, et le moment angulaire (moment cinétique) d'autre part.
L'énergie mécanique (cinétique dans ce cas) peut se conserver ou pas. Dans les collisions élastiques, elle se conserve. Dans les autres, une partie est transformée en chaleur. Par exemple la collision entre billes d'acier est presque élastique et celle entre deux masses de beurre est totalement inélastique.
J'imagine que pour vous le choc est élastique. C'est à dire qu'il n'y a pas d'énergie cinétique transformée en chaleur.
Je ne peux pas vous faire un cours ici. Mais je vous conseille de télécharger ce fascicule (7 Mo):
http://www.sendspace.com/file/ttrwye Cliquez sur: Click here to download from freespace.
et de lire les chapitres 6, 7 et 9 (et peut-être aussi le 8).
Puis de revenir ici pour éclaircir ce qui sera resté incompris.
Au revoir.

[Petipo]

Bonjour,
merci pour cette précieuse aide. Après lecture des chapitres 6,7 et 9 j'éprouve tout de même quelques difficultés à trouver la bonne approche pour résoudre ce problème. Je pense avoir compris qu'il me faut utiliser la conservation de l'énergie et du moment cinétique mais je ne sais trop comment procéder dans ce cas précis.
Je crains de me perdre dans des calculs qui ne mènent à rien et mon absence totale de connaissances en mécanique constitue un assez lourd handicap. J'ai envisagé de ramener cette collision (élastique) à une collision entre 2 particules (l'une des particules étant alors "virtuelle", située sur la ligne au point d'impact) sans trop de succès, c'est très probablement assez débile comme approche.
Serait-il possible d'avoir un poil plus de précision sur les équations à utiliser ?

[LPFR]

Bonjour.
La collision d deux particules en 2D est indéterminée car il faut un paramètre qui indique la "frontalité" du choc. Vous pouvez calculer les vitesses en fonction de la direction de sortie d'une des particules, mais c'est tout.
Dans votre cas, cette "frontalité" dépend de l'endroit où la particule percute la barre entre les deux autres et de l'angle de cette barre au moment du choc.
On peut admettre que l'angle de réflexion de la particule contre la barre obéit à la loi de réflexion dans les miroirs: angle de réflexion égal à angle d'incidence.
Il faut donc commencer par trouver la position de la barre au moment du choc (ce n'est pas si simple).
Ceci fixe la direction de départ de la particule.
Maintenant il faut ajouter les autres conditions: conservation de l'énergie, du moment linéaire et moment angulaire.
Il faut déjà calculer le moment angulaire:
- de la particule: C'est le produit du moment linéaire de la particule par le "son bras de levier". C'est à dire la distance entre le point de référence et la droite qui porte la vitesse de l particule.
- des deux masses et la barre: c'est le moment linéaire du centre de masses de la barre en prenant la masse totale de la chose multiplié par le "bras de levier" de la droite qui le porte. Plus le moment angulaire des deux particules autour du centre de masses de la chose.

Pour les énergies c'est la somme des énergies de translation plus l'énergie de rotation de la chose.

Mais essayez déjà de trouver l'endroit, le temps et la position de la chose au moment du choc. Je viens de réfléchir un peu et ce n'est pas simple du tout. Il peut avoir plusieurs solutions mathématiques et il faut choisir la bonne... s'il y en a une. Car il est parfaitement possible que la rotation fasse que la chose "esquive" la particule grâce à se rotation.

Tout compte fait, le problème est assez compliqué.
Au revoir.

[A voir en vidéo sur Futura]

[Petipo]

En ce qui concerne le temps et les positions des masses au moment de l'impact j'ai déjà résolu le problème, enfin je crois bien. Comme il s'agit d'une simulation informatique (avec discrétisation du temps donc), je calcule le temps T pour lequel grâce aux coordonnées et vitesses des 3 masses au pas de temps précédent. Ainsi, si je trouve que les 3 masses seront alignées à un instant T avant le pas de temps suivant (et que 0<=k<=1), je sais qu'il y a collision et je peux en connaitre les coordonnées exactes (les vitesses au moment de l'impact restent inchangées).

Il faut déjà calculer le moment angulaire:
- de la particule: C'est le produit du moment linéaire de la particule par le "son bras de levier". C'est à dire la distance entre le point de référence et la droite qui porte la vitesse de l particule.

J'avoue ne pas être certain de bien comprendre cette phrase. De quel point de référence parlons-nous ?
Encore merci pour l'aide et désolé si je pose quelques questions idiotes.

[LPFR]

Re.
Il ne suffit pas que les trois masses soient alignées pour que la particule touche la barre. Il faut encore que la particule soit entre les deux masses des extrémités.
Et le fait que le temps soit discret dans la simulation ne vous permet pas de faire le calcul au temps discret. Il faut le faire au moment du choc.
De même que quand une particule rebondit sur une paroi, il faut tenir compte dans la simulation que le choc a eu lieu entre deux phases de calcul et à une coordonnée intermédiaire. Dans ce cas c'est très simple. Dans le cas que vous voulez calculer, c'est la même chose mais en plus compliqué.

Oubliez la phrase (elle est correcte). Puisque vous travaillez avec des vecteurs, utilisez la définition vectorielle. Le calcul donne la même chose, même si on "voit" le résultat moins facilement.

Quand vous calculez le moment angulaire, vous le faites par rapport à un point. Souvent c'est le centre de masses des objets. Mais pas ici. Le moment angulaire de la particule, comme celui des deux masses, doit être calculé par rapport à un point (quelconque) de référence. Le même avant et après le choc.
A+

[Petipo]

Ok, merci, je vais voir ça. Par contre, je vérifie bien que la particule soit entre les deux masses via 0<=k<=1. De plus, je ne fais pas le calcul au temps discret mais prends simplement les valeurs de vitesses et coordonnées à chaque pas de temps pour ensuite "interpoler" en temps continu "entre" ces pas de temps et j'ai donc un temps et des coordonnées "intermédiaires".