Bonsoir à tous, je suis actuellement en train de faire un exercice d'optique géométrique et je bloque à partir de la 3ème question.
Voici l'énoncé :
-Deux morceaux de verre (d’indices de réfraction différents), sont respectivement taillés en
forme de triangles rectangle (ADB) et isocèle (ABC). Les indices de réfraction des verres sont
de N pour le triangle rectangle, et n pour le triangle isocèle.
et voici le reste ::
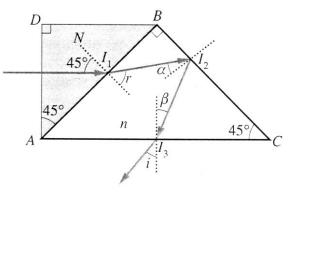
Un rayon lumineux arrive sous incidence normale par la face AD du système ainsi constitué.
On s’intéresse pour ce rayon à la réfraction en I1, à la réflexion en I2, et enfin à la réfraction en
I3. Les valeurs des indices des deux triangles sont telles que la reflexion soit totale en I2.
1)écrire la relation de Snell-Descartes aux points I1 et I3.
2)écrire une relation entre les angles r et , et entre les angles et .
3)trouver la relation entre n et N que l’on peut déduire de l’angle limite de réfraction
en I2.
4)calculer alors, lorsque cette condition est réalisée, N, r, , , et i si n=3/2.
5)on appelle N0 cette valeur limite de N. Pour que la reflexion soit totale en I2, N doit
il être plus grand ou plus petit que N0 ?
6)écrire la relation vérifiée par N et n pour que l’angle i soit nul, et calculer alors N.
Pour la 1), c'est pas compliqué, en I2 on a : N sin(45)=n sin r et en I3 on a : n sin(beta) = sin i
2) On prolonge les normales en I1 et I2 et on trouve facilement que r+A = pi/2
Pour alpha et beta, dans le triangle I2CI3, on a (90-alpha)+(90-beta)+45=180 pour arriver au final à : alpha + beta = pi/4
3) à partir de cette question-ci, je bloque, j'ai juste posé l'angle critique en I2 qui est de sin(alpha)=Nair/n (soit 1/n)
Je cherche juste de l'aide pour cette question, sachant que la suite de l'exercice en dépend.
Merci d'avance !
-----