La transformée de Fourier pour les nuls

[b@z66]

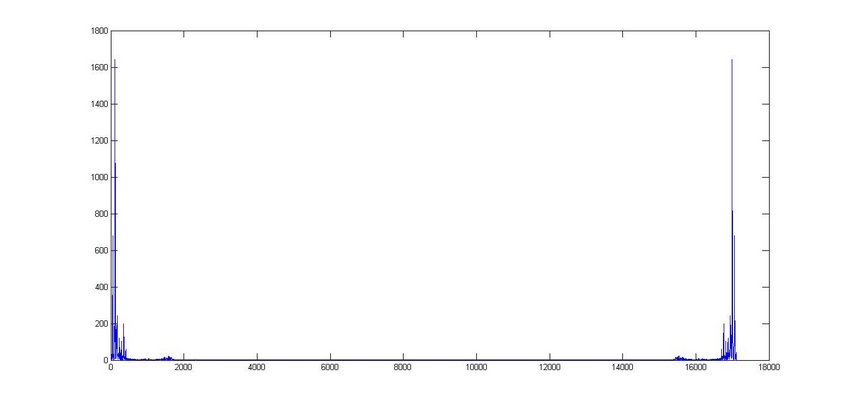
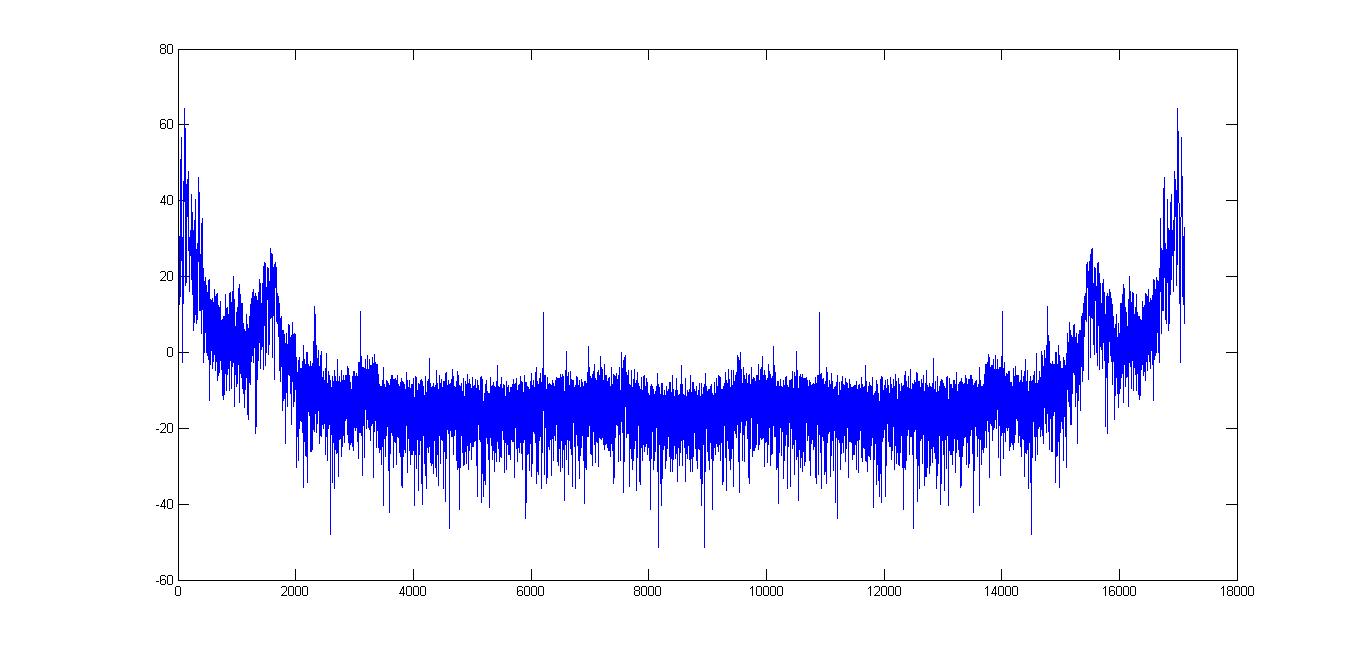
Ou encore, on a souvent l'habitude, en pratique, d'appeler "spectre" le dessin du module d'une transformée de Fourier représentée pour ses fréquences positives uniquement(le module d'une TF de signal réel étant paire sur l'axe des fréquences). Toutefois, la seule information du module ne suffit pas à caractériser entièrement le signal temporel. Il faut aussi tenir compte de l'argument et c'est ce qui devrait être fait systématiquement pour caractériser entièrement un signal mais, il faut bien reconnaitre, on résume souvent abusivement le spectre à son seul module(sans doute parce que le principal intérêt des procédés de filtrage utilisés dans le multiplexage fréquentiel est souvent d'agir sur le module).
-----

[Wenneguen]

Pourtant, le spectre que m'affiche Audacity n'est visiblement pas paire ; quelle en est la raison ? Est-ce que seule la première moitié est conservée ?

[b@z66]

Pourtant, le spectre que m'affiche Audacity n'est visiblement pas paire ; quelle en est la raison ? Est-ce que seule la première moitié est conservée ?

C'est ce que je dis, Audacity ne montre pour son spectre que la partie positive des fréquences(normal puisque l'information sur les fréquences "négatives" est redondante). Si Audacity affichait égalément les fréquences négatives du spectre à la manière d'une transformée de Fourier classique, vous verriez un spectre dont le module est pair. Dernière chose, un spectre est justement représenté en pratique avec des fréquences positives contrairement à la TF qui montre également les fréquences négatives(qui peuvent paraitre moins "physiques" à certains) mais cela ne fait au final aucune différence puisque, comme je l'ai dit plus haut, l'information de la TF sur les fréquences négatives est redondante de celle sur les fréquences positives dans le cas d'un signal usuel, c'est à dire mathématiquement réel.

[Wenneguen]

D'accord merci je commence à mieux comprendre J'en profite pour poser une nouvelle question ; voici le module de la fft de mon signal :



L'axe des abscisses représente donc les fréquences si j'ai bien compris. Comment associer à chaque abscisse x la fréquence en Hz correspondante ? Car sur cet axe Matlab s'est contenté de conserver la numérotation des échantillons du signal (j'avais bien un signal d'environ 17 000 échantillons).

[b@z66]

D'accord merci je commence à mieux comprendre J'en profite pour poser une nouvelle question ; voici le module de la fft de mon signal :

Pièce jointe 220768

L'axe des abscisses représente donc les fréquences si j'ai bien compris. Comment associer à chaque abscisse x la fréquence en Hz correspondante ? Car sur cet axe Matlab s'est contenté de conserver la numérotation des échantillons du signal (j'avais bien un signal d'environ 17 000 échantillons).

Le spectre(en FFT) de ton signal est celui de ton signal "échantillonné", c'est à que tu peux négliger la répétition du spectre vers l'échantillon 17000: cette répétition est due au processus d’échantillonnage du signal d'origine et non au signal d'origine lui-même. Tu pourrais donc zoomer sur les 4000 premiers échantillons apparemment. Concernant l'incrément fréquentiel dû aux différents échantillons, tu peux le calculer en faisant: 1/Durée totale de l'analyse en temporel. Enfin, représenter l'axe des ordonnées de ton spectre avec une échelle logarithmique permet souvent de mieux mettre en évidence les différents ordres de grandeurs(un rapport de 1 à 100(ou 1000) entre deux amplitudes y apparait beaucoup mieux).

[Wenneguen]

Merci mais je ne suis pas sûr de bien comprendre, par " répétition " tu entends " symétrie " ? Qu'est-ce qui motive qu'on ne conserve que les 4000 premiers échantillons ? Pourquoi pas 5000 ou 8500 par exemple ?

Voici le module de la transformée de Fourier en décibels

module_fourier_dB=20*log10(  abs( fft(mon_signal) )  )

En le calculant comme tu me le suggères, l'incrément fréquentiel vaut 2,58 Hz. Est-ce à dire que le kème échantillon correspond à la fréquence k*2,58 Hz ?
Qu'en est-il des fréquences négatives dont tu parlais ?

Merci beaucoup pour ton aide en tout cas

[b@z66]

Merci mais je ne suis pas sûr de bien comprendre, par " répétition " tu entends " symétrie " ? Qu'est-ce qui motive qu'on ne conserve que les 4000 premiers échantillons ? Pourquoi pas 5000 ou 8500 par exemple ?

Voici le module de la transformée de Fourier en décibels

module_fourier_dB=20*log10(  abs( fft(mon_signal) )  )

Pièce jointe 220896

En le calculant comme tu me le suggères, l'incrément fréquentiel vaut 2,58 Hz. Est-ce à dire que le kème échantillon correspond à la fréquence k*2,58 Hz ?
Qu'en est-il des fréquences négatives dont tu parlais ?

Merci beaucoup pour ton aide en tout cas

Tu n'as du pas eu de cours de traitement de signal et en particulier sur l’échantillonnage? Par "répétition", j'entends bien "répétition" ou encore "périodisation" car c'est ce que produit le processus d’échantillonnage: ce processus recopie le spectre du signal d'origine sur l'axe des fréquences tout les Fe(Fe étant la fréquence d'échantillonage: c'est à dire que tu a toujours ton spectre centré autour de la fréquence 0 mais aussi ce même spectre reproduit autour de la fréquence Fe, 2Fe, 3Fe... et même en considérant les fréquences négatives autour de -Fe, -2FE,-3Fe... Pour ta question concernant le kème échantillon, la réponse est oui. D'ailleurs on doit en déduire que ta fréquence d'échantillonage est de 42KHz environ(17000x2,58) car le dernier échantillon de ta FFT correspond à la fréquence Fe normalement: c'est justement à cause de ce phénomène de "périodisation", que tu retrouves autour de cette fréquence le même spectre que celui centré autour de la fréquence 0(en fait la forme que tu observe autour de 17000 correspond à la forme du spectre d'origine mais pour les fréquences négatives, c'est pour cela que tu retrouver une certaine symétrie qui ici se manifeste avec un axe en Fe/2). Mais encore une fois cela n'est qu'un "artefact" du processus d'échantillonage et si au fond c'est uniquement le spectre du signal d'origine qui t'intérersse, tu te débarasses de tout ce qui est des fréquences supérieures à Fe/2 (ta FFT donnant les résultats pour les fréquences de f=0 à f=Fe). Pour ce qui est de garder les 4000 premiers échantillons, c'est qu'au delà on atteint le plancher du "bruit" de mesure(la zone plate au milieu de ton graphe) et que ce bruit ne peut pas vraiment t'informer sur ton signal puisqu'il est du uniquement aux incertitudes de ton processus de mesure.

[b@z66]

PS: si tu veux vraiment te représenter l'allure du spectre de ton signal échantilloné(que ce soit pour les fréquences négatives ou positives jusqu'à l'infini), tu n'as qu'à considérer le motif de ce graphe répété tous les Fe car ta FFT ne te montre finalement qu'une période de ce spectre qui est en réalité périodique sur l'axe des fréquences.

[Stksousou]

Bjr! Pouvez vous démontrer l'existence d'un point de symétrie d'une transformée de fourier discrète s'agissant de la symétrie hermitienne?merci

[JPL]

Intervention inutile sur une discussion qui date de quatre ans.

[sylvestrel]

Voici en pièce jointe, un algo à ouvrir dans ALGOBOX (petit logiciel gratuit et remarquable installation et prise en main rapide) après avoir changé l'extension .txt en .alg signature d'ALGOBOX (le .alg n'était pas reconnu…).
J'espère que ça fonctionnera et répondra à la demande.

Sylvestrel

Pièce jointe supprimée

[JPL]

Merci de poster le code dans un message entre les balises [Code]...[/Code] au lieu d’utiliser un fichier txt.