Nouvelle question de physique

[Amanuensis]

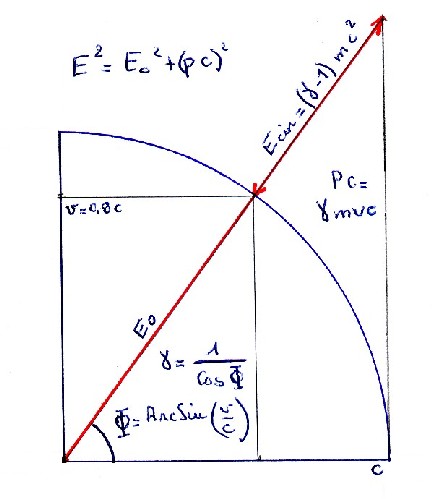
Ben si quand même. Dans le cadre de la relativité, l'énergie cinétique d'une 4-impulsion P, relativement au "référentiel" U, est (au carré): (P.U)²-P²=E²-m² (1), ce qu'on peut interpréter comme l'énergie (au carré) moins l'énergie de masse (au carré), et donc comme la partie du carré de l'énergie qui est "due" au mouvement relativement au référentiel.

Sûr qu'on peut se passer de la notion d'énergie cinétique, dont la fonction est essentiellement de se 'raccrocher' à la mécanique classique.

Il est sûrement stérile de débattre si l'énergie cinétique d'un 4-vecteur énergie-impulsion est liée au mouvement relatif, c'est plutôt une évidence, non?

(1) L'énergie est P.U, la quantité de mouvement la projection P-(P.U)U, dont la norme est (P.U)²-P²
-----

[curieuxdenature]

Si E n'est pas totalement cinétique, les voiles solaires seront encore moins performantes car elles encaissent la quantité de mouvement des photons.

Bonjour

Selon la relativité, on ne peut pas parler d'énergie cinétique pour un photon.
Il suffit de regarder le triangle relativiste pour s'en convaincre, la partie cinétique ne peut se calculer qu'en présence d'une particule massive et de vitesse inférieure à c :
pour une particule massive, la tangente de l'angle Théta donne une valeur infinie à l'énergie cinétique, et ce qui n'est pas le cas du photon puisque sa masse est nulle.


En ce qui concerne la quantité de mouvement d'un photon, le transfert d'énergie via une voile solaire se calcule comme pour la propulsion d'une fusée :
Accélération = (E / c) * (1 / m)
E l'énergie totale des photons reçue par seconde, m la masse de l'ensemble voile + fusée.
E / c est une quantité de mouvement sans faire appel à la masse, ici E = n * hv, n étant le nombre de photons.

[Amanuensis]

Selon la relativité, on ne peut pas parler d'énergie cinétique pour un photon.

Pourquoi la définition E²-m² pour le carré de l'énergie cinétique ne serait pas acceptable? (écriture avec c=1)

(la figure est simplement pas assez générale.)

[Amanuensis]

Par ailleurs, pour le cas du champ électromagnétique, il me semble qu'on pourrait proposer la norme (spatiale) du vecteur de Poynting pour la densité volumique d'énergie cinétique dans un référentiel donné.

D'autres opinions sur ce point?

[invite57f37970]

Pourquoi la définition E²-m² pour le carré de l'énergie cinétique ne serait pas acceptable? (écriture avec c=1)

(la figure est simplement pas assez générale.)

Mais ça ne redonne pas à la limite non-relativiste ? A moins que la formule ne soit supposée s'appliquer qu'au cas de masse nulle ?

[curieuxdenature]

Pourquoi la définition E²-m² pour le carré de l'énergie cinétique ne serait pas acceptable? (écriture avec c=1)

(la figure est simplement pas assez générale.)

Bonjour

parce que l'énergie cinétique est associée à la masse d'une particule au repos et que le photon n'est jamais au repos.
Pourquoi n'est-il jamais au repos ?
- Parce que sa masse est nulle.

M'enfin bref, à la limite on pourrait aussi se poser la question de la pertinence du terme "particule" pour nommer le photon...
Si je conçois le photon comme une excitation du champ électromagnétique, il ne me viendrait pas à l'idée de parler de masse d'une onde acoustique ou d'une onde scélérate (une vague).
Bein oui, quand je mets mon ampli à fond, les vitres tremblent, donc les ondes sonores ont une masse et une énergie cinétique.
Je peux même donner une grandeur chiffrée.
Conclusion bizarre, n'est-ce pas ?

Mais, si je veux persister à dire que le photon est une particule, alors je dois aussi penser que les particules élémentaires sont les excitations d'un champ.
Des résonances particulières, un peu comme des petits circuits LC accordés sur une fréquence bien spécifique.
Admettons, mais alors, pourquoi ces résonances ne se déplacent-elles pas à la vitesse de la lumière ?
- Parce qu'elles ont une masse.

Quelqu'un pour se farcir la suite ? (pourquoi elles ont une masse.)

[Amanuensis]

Annulé......

[Amanuensis]

Mais ça ne redonne pas à la limite non-relativiste ?

Bon point... La définition usuelle donnant la limite est Ec = E - mc², pas la différence des carrés. Cela fait un facteur 2 à la limite non relativiste.

Il me semblait qu'il y a avait une formule pour les deux cas, malgré le fait que m=0 n'est pas la même chose que la limite m -> 0. Vais réfléchir...

[invite57f37970]

Bon point... La définition usuelle donnant la limite est Ec = E - mc², pas la différence des carrés. Cela fait un facteur 2 à la limite non relativiste.

Il me semblait qu'il y a avait une formule pour les deux cas, malgré le fait que m=0 n'est pas la même chose que la limite m -> 0. Vais réfléchir...

Je crois qu'il y a aussi la puissance de v qui ne va pas à la limite non-relativiste dans ta proposition initiale puisque ça donnerait pc = mvc + ... . Par contre

m'a l'air de "marcher" dans tous les cas, si on veut bien parler d'Ec d'un photon bien sûr...

[invite57f37970]

il ne me viendrait pas à l'idée de parler de masse d'une onde acoustique

Et les phonons ?

[Amanuensis]

Par contre

m'a l'air de "marcher" dans tous les cas

C'est l'usuelle. J'avais l'idée fausse (et n'ai pas revérifié) qu'elle ne marchait pas pour m=0.

, si on veut bien parler d'Ec d'un photon bien sûr...

Je ne comprends pas le débat, comme je l'ai écrit plus tôt. C'est juste une question de définition, non?

Je crois qu'il y a aussi la puissance de v qui ne va pas à la limite non-relativiste dans ta proposition initiale puisque ça donnerait pc = mvc + ... .

???

[invite57f37970]

Quelqu'un pour se farcir la suite ? (pourquoi elles ont une masse.)

Parce que le champ lui-même a une masse et vérifie une équation libre du style ?

Je ne comprends pas le débat, comme je l'ai écrit plus tôt. C'est juste une question de définition, non?

Oui, et comme toutes les questions de définitions, on peut en discuter à l'infini

???

Ta proposition initiale pour l'énergie cinétique donne dans tous les cas je veux dire.