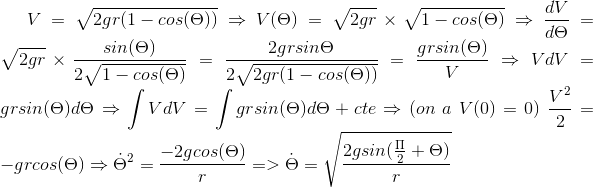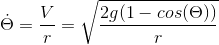Particule glissant sur une sphère

[Fatzeyk]

Bonjour,

Une particule de masse m se met à glisser, sans frottement, à partir du sommet A d'une sphère immobile de rayon R.

1 - Représenter et calculer, en fonction de R, g et q, la vitesse de la particule au point M.
Là j'ai appliqué le théorème de l'énergie cinétique puis j'ai trouvé CodeCogsEqn(2).gif

2 - Représenter la force exercée par la sphère sur le mobile et calculer sa valeur en fonction de m, g et q.

Là en appliquant le 2ème loi du Newton et en projetons la relation sur la normale de Frénet j'ai trouvé : CodeCogsEqn(3).gif

3 - Calculer gif.latex.gif en fonction de CodeCogsEqn(1).gif.

Là j'ai essayé de dériver CodeCogsEqn(4).gif et puis trouver gif.latex.gif = -1/sin(CodeCogsEqn(1).gif) mais mon prof m'a dit que c'est faut
puis j'ai essayé en utilisant gif.latex.gif = V/r mais c'est faut aussi

si quelqu'un peut m'aider et merci
-----

[LPFR]

Bonjour et bienvenu au forum.
Votre prof a raison.
Si votre formule était correcte, cela veut dire que la variation de thêta avec le temps (la vitesse angulaire de la particule) serait infinie au départ. Alors que c'est l'inverse. La vitesse est nulle au départ.
Morale: il faut toujours regarder le sens physique des équations. Et s'alarmer si on a des variables qui peuvent annuler un dénominateur.
Au revoir.

[Fatzeyk]

Bonsoir,
Bon voilà c'est que j'ai essayé :



Je ne sais pas si c'est correct ou j'ai fait n'importe quoi

[LPFR]

Bonjour.
En physique il n'y a jamais d'intégrales indéfinies.
Il n'y a que les profs de maths qui font ça, quand ils officient en profs de physique. Les physiciens ne le font pas.

Si, au lieu de faire l'intégrale comme intégrale indéfinie à une constante près, vous preniez l'habitude de faire (en physique) que des intégrales définies entre bornes, vous n'auriez pas fait l'erreur que vous avez faite. Vous venez de trouver que pour thêta = 0, V n'est pas zéro.
Intégrez le terme de gauche entre 0 et V et celui de droite entre 0 et thêta.
Au revoir.

[A voir en vidéo sur Futura]

[Fatzeyk]

Bonsoir,

Bon, j'ai ressayé :

CodeCogsEqn(8).gif

et avec quelques relations du math CodeCogsEqn(9).gif

Puis, en remplaçant: CodeCogsEqn(10).gif

en attendant ta réponse, merci pour ton aide

[LPFR]

Re?
Non. Ce n'est pas mieux.
Vous ne pouvez pas intégrer quelque chose qui n'a pas de différentiel comme

Il vous faut un différentiel:

ou


Et quel est l'intérêt de calculer d'une façon si indirecte et longue ?
A+

[Fatzeyk]

Re,

- On peut multiplier les deux termes par dt pour que ça soit correcte?

- Pour :

J'ai déjà essayé mais mon prof m'a dit que ce n'est pas correcte

A+

[LPFR]

Re,

- On peut multiplier les deux termes par dt pour que ça soit correcte?

- Pour : Pièce jointe 244518

J'ai déjà essayé mais mon prof m'a dit que ce n'est pas correcte

A+

Bonjour.
Eh bien, je vous dis que c'est correct.
EDIT. Mais que ce n'est pas nécessaire de faire de calculs aussi longs.
La perte de hauteur est h= r(1 - cos(thêta)) et la vitesse acquise par perte d'énergie potentielle est h = sqrt(2gh).
Yaka substituer.

Au revoir.

[Fatzeyk]

Re,

Je n'ai pas bien compris comment faire ta méthode, j'utilise l'énergie potentielle mais sans rien trouver.

[LPFR]

Bonjour.
Il y a une faute de frappe dans mon dernier message. J'ai écrit h = sqrt(2gh) à la place de V = sqrt(2gh).
Une fois que vous avez V, la vitesse angulaire est simplement V/r.
Et la particule reste en contact avec la sphère aussi longtemps que la composante du poids de la particule, perpendiculaire à la surface de la sphère, est plus grande que la force centrifuge.
Le problème est très simple et ne demande que des calculs simples. Pas d'intégrales ni d'équations différentielles.
Mais il faut rester dans la physique au lieu de se noyer dans les équations.
Au revoir.

[Fatzeyk]

Bonjour,

J'ai déjà essayé V/r mais mon prof m'a dit que c'est aussi faut et qu'il faut faire une autre projection
Bon pas grave, merci pour ton aide

Je te souhaite une bonne journée