Bonjour
Je dois réaliser, dans le cadre d'un mini-projet de maths, la résolution numérique d'une EDP elliptique, mais j'aimerais si possible éviter de traiter de la fameuse membrane élastique avec son équation de Poisson.
De façon absolument indépendante, je m'intéresse depuis peu de temps aux phénomènes liés à la capillarité, j'ai d'ailleurs commencé à lire Gouttes, bulles, perlets et ondes de Quéré, Brochard-Wyart et de Gennes (j'adore !).
J'aimerais lier les deux, en résolvant numériquement une équation issue de cette belle physique des surfaces.
Seulement j'ai besoin de votre aide.
Voilà la problématique que je voudrais poursuivre: quelle est la surface perturbée d'un plan d'eau dans lequel plonge une "fôret" de fibres ?
Cela m'est inspiré de la lecture de l'ouvrage déjà cité.
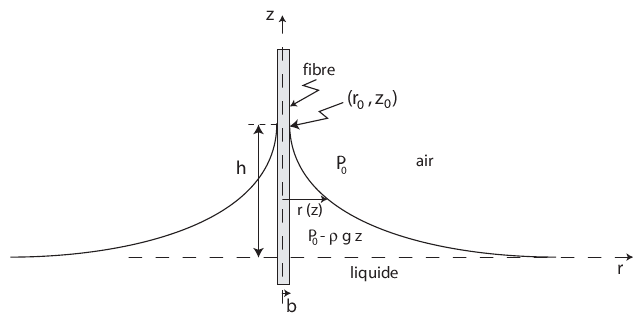
Prenons d'abord le cas d'une seule fibre, de rayon b, plongée dans de l'eau.
Il est mentionné que loin de cette distance capillaire, la fibre crée une perturbation de la surface décrite par l'équation en deux dimensions
.
On peut la comprendre à une dimension en disant que la courbureloin du ménisque est faible donc s'approche par
, et que l'égalité des pressions hydrostatique et de Laplace donne
.
D'autres calculs sont menés, notamment celui de la hauteur estimée du ménisque.
Cliquez pour afficher
Bilan: J'obtiens bien une EDP elliptique qui modélise la perturbation de la surface de l'eau loin d'une fibre, mais il me manque des conditions aux limites pour pouvoir en faire quoique ce soit. Or, étant dans une zone(loin relativement à la longueur capillaire du fluide), je ne sais pas que dire des conditions proche de la fibre ! (à l'infini, l'altitude est nulle)
Auriez vous des pistes pour pouvoir exploiter cette modélisation ?
Si c'est le cas, j'aimerais essayer de généraliser ça (dans un second temps) à une situation de plusieurs fibres disposées dans l'eau (de façon convenable, c'est à dire notamment éloignées de quelques longueurs capillaires au minimum).
Un grand merci d'avance à ceux qui me liront et décideront de m'aiguiller !
PS: si vous pensez que c'est une reflexion vouée à l'échec ou idiote faîtes m'en part. Je suppose que cet effet de perturbation est très léger pour une fibre mais pour plusieurs ... ?
PS bis: pour la condition aux limites recherchée, j'avais pensé à utiliser la hauteur du ménisque. Sauf qu'à cet endroit l'équation elliptique ne modélise absolument pas la surface.
Egalement j'avais pensé à regarder la conservation du volume pour estimer l'altitude moyenne à une distancede la fibre. Sauf qu'en travaillant en plan d'eau "infini" cela ne marche pas (le volume ne se quantifie pas). Peut être travailler dans une "flaque restreinte" (mais pas trop, sinon je crois savoir que d'autres phénomènes se produisent pour une trop faible épaisseur, pression de disjonction, longueur de cicatrisation, etc... et puis la deuxième condition aux limites se complexifie du même coup).
-----