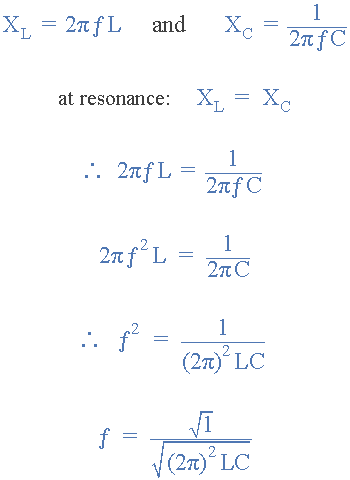Démonstration d'une formule : circuit LC (résonance)

[Flibusterie]

Salut à tous!

J'étudie en ce moment le circuit LC donc je connais mes formules mais j'ai du mal à les retrouver par moi-même.
Par soucis de perfectionnisme j'aimerais être capable de les démontrer par moi même.

Là où je bloque c'est au niveau de la fréquence de résonance :

Comment fait-on pour passer de la formule de la pulsation
3435abe1d8cb30fca9c35b039cd2a78b.png
à celui de la fréquence
b32173d818ca13fb30285ce418722da3.png

Je ne sais pas trop comment m'y prendre...
J'ai fait quelques essais sans retrouver la solution.
Faut-il utiliser une équation de trigonométrie ou bien faire une simple élévation au carré ?
-----

[DuckDDR]

Bonjour,

Je ne vois pas exactement ce que tu recherches, une fois que tu as la pulsation, pour retrouver la fréquence tu utilises juste que .

EDIT: C'est d'ailleurs ce qui est écrit dans ton .png. Peut être dois-tu préciser ta question...

[Nicophil]

Salut,

Comment fait-on pour passer de la formule de la pulsation à celui de la fréquence ?

Ben en divisant par radians quoi...

[Flibusterie]

Je ne vois pas exactement ce que tu recherches, une fois que tu as la pulsation, pour retrouver la fréquence tu utilises juste que .

EDIT: C'est d'ailleurs ce qui est écrit dans ton .png. Peut être dois-tu préciser ta question...

Oui effectivement.

Je crois comprendre qu'il faut utiliser cette formule pour passer d'une formule à l'autre.
Donc f0 et w0 corespondent aux points où les réactances inductive et capacitive sont égalent.

Il faut forcément trouver les réactances sur un graphique ou avec une équation complexe, non ?

Ben en divisant par radians quoi...

Oui, ça semble simple dit comme ça.
J'ai bêtement bloqué sur le racine de 1, je n'avais pas pensé à y lui retirer sa racine.

[A voir en vidéo sur Futura]

[DuckDDR]

Donc f0 et w0 corespondent aux points où les réactances inductive et capacitive sont égalent.

Exactement.

Il faut forcément trouver les réactances sur un graphique ou avec une équation complexe, non ?

Un système d'équation obtenu à partir de l'impédance suffit. Tu connais l'impédance du condensateur et celle de la bobine leurs parties imaginaires sont respectivement égales à la réactance capacitive et à la réactance inductive. De là on remplace la fréquence par la fréquence de résonance et on montre qu'elles sont égales. Sinon il suffit de voir que l'impédance du circuit est nulle à la résonance et ça fait le café

[DuckDDR]

Sinon il suffit de voir que l'impédance du circuit est nulle à la résonance et ça fait le café

... seulement si tu es en LC série, pardon ...

[Flibusterie]

Ok, je commence à y voir clair :

En prenant un condensateur de 25nF à une fréquence de 4KHz, j'utilise la formule de la réactance

je trouve Xc = 1592 ohm.

Je cherche un circuit en résonance donc je peux prendre Xc = Xl.
Donc je trouve que l'inductance de ma bobine devra être de 63 mH.


Maintenant une dernière question;
quand on compense les pertes d'énergie à chaque demi-période, en ajoutant une impulsion avec un transistor par exemple, est qu'il y un moment précis où envoyer l'impulsion?
Qu'est ce que ça change qu'on envoie l'impulsion au moment où le condensateur est plein? Ou quand la bobine est pleine? Ou quand les 2 sont à moitié remplis ?

[DuckDDR]

Donc je trouve que l'inductance de ma bobine devra être de 63 mH.

Je confirme.

quand on compense les pertes d'énergie à chaque demi-période, en ajoutant une impulsion avec un transistor par exemple, est qu'il y un moment précis où envoyer l'impulsion?
Qu'est ce que ça change qu'on envoie l'impulsion au moment où le condensateur est plein? Ou quand la bobine est pleine? Ou quand les 2 sont à moitié remplis ?

Pourquoi à chaque demie-période? Je pense que si tu fournis de l'énergie à chaque demie-période tu doubles la fréquence avec laquelle oscille l'énergie nan?
Pour moi si la résistance interne de ton circuit vaut la puissance que doit fournir ton dispositif d'entretien est (effet Joule) donc que la tension aux bornes de celui-ci doit être avec les grandeurs sinusoidale on obtient ce qui prouve que les deux signaux doivent avoir la même fréquence d'oscillation et la même phase.

[Flibusterie]

Oui, je n'avais pas pensé à ça.
À quoi correspond le + phi dans la formule de i(t)?

En fait je demandais ça car au détour d'un lien que j'ai malheureusement perdu, j'avais lu qu'en augmentant le signal à chaque cycle, selon qu'on le faisait alors qu'est plein la bobine ou le condo, cela pouvait augmenter soit la tension, soit le courant.
Le même principe qu'un transformateur ou un boost.

[DuckDDR]

À quoi correspond le + phi dans la formule de i(t)?

correspond à la phase à l'origine du signal, lorsque le signal peut être nul, maximal etc ... il peut occuper toute les valeurs comprises entre son minimum et son maximum d'amplitude. Maintenant pour les signaux sinusoïdaux qui nous concernent, tu vois que la synchronisation de fréquence n'est pas la seule condition, les signaux doivent avoir la même phase (sinon ils pourraient se compenser pour un déphasage de par exemple).

En fait je demandais ça car au détour d'un lien que j'ai malheureusement perdu, j'avais lu qu'en augmentant le signal à chaque cycle, selon qu'on le faisait alors qu'est plein la bobine ou le condo, cela pouvait augmenter soit la tension, soit le courant.
Le même principe qu'un transformateur ou un boost.

Clairement, mais cela dépend ce que tu recherches, moi je partais du principe que tu voulais entretenir les oscillations du LC (en pratique un RLC) en compensant les pertes par effet Joule dues à la résistance interne du circuit. Parce qu'en injectant un signal synchronisé et en phase avec la bonne amplitude, après un petit régime "bizarre" le temps que les charges et décharges s'accordent avec le signal d'entretien, le régime sera bien périodique.

[curieuxdenature]

En fait je demandais ça car au détour d'un lien que j'ai malheureusement perdu, j'avais lu qu'en augmentant le signal à chaque cycle, selon qu'on le faisait alors qu'est plein la bobine ou le condo, cela pouvait augmenter soit la tension, soit le courant.
Le même principe qu'un transformateur ou un boost.

Bonjour

c'est plus qu'un transformateur, on a besoin de compenser les pertes en amplifiant le signal.
Pour ça on prélève une partie de la sinusoide du circuit LC et on la réinjecte dans le transistor, puisque le montage amplifie le courant le circuit se met à osciller si bien qu'on peut en prélever une bonne partie sans que ça s’arrête.

Le schéma de principe est assez simple à comprendre, à la mise sous tension le transistor conduit et une oscillation prend naissance dans LC.
Un enroulement secondaire, branché dans le bon sens, envoie une petite partie du courant dans la base et l'entretien de l'oscillation démarre.
Correctement calculés, l'oscillateur est particulièrement stable et facile à faire fonctionner. Je dirais même que c'est le montage le plus facile à faire osciller pour un débutant du fer à souder.

Comme tu peux le constater, on ne demande pas à quel moment L ou C est chargé ou déchargé, la réinjection se fait en phase avec le signal de base.

[AOBII]

Il te suffit de transformer ton équation en élévant les deux membres au carré sachant que f=1/w

[AOBII]

rectification f=w/2pi

[stefjm]

quand on compense les pertes d'énergie à chaque demi-période, en ajoutant une impulsion avec un transistor par exemple, est qu'il y un moment précis où envoyer l'impulsion?
Qu'est ce que ça change qu'on envoie l'impulsion au moment où le condensateur est plein? Ou quand la bobine est pleine? Ou quand les 2 sont à moitié remplis ?

Bien sûr que cela change quelque chose : Il faut le faire en phase, à la bonne fréquence et au bon moment.

Comme tu peux le constater, on ne demande pas à quel moment L ou C est chargé ou déchargé, la réinjection se fait en phase avec le signal de base.

Sauf que tu donnes un exemple de système oscillant avec asservissement de l'oscillation et donc un système qui injecte quand il le faut. (automatiquement)

On peut voir le transistor comme un rebouclage d'une grandeur de sortie sur l'entrée. La comparaison de tension est faites par une maille.
S'il y a un gain suffisant, le bruit est amplifié et cela oscille à la fréquence de résonance du circuit LC.
Cordialement.

[curieuxdenature]

Sauf que tu donnes un exemple de système oscillant avec asservissement de l'oscillation et donc un système qui injecte quand il le faut. (automatiquement)

On peut voir le transistor comme un rebouclage d'une grandeur de sortie sur l'entrée. La comparaison de tension est faites par une maille.
S'il y a un gain suffisant, le bruit est amplifié et cela oscille à la fréquence de résonance du circuit LC.
Cordialement.

Bonjour

avec un circuit LC on se doute que le signal sera une sinusoïde, il n'y a pas beaucoup de montages pratiques qui travaillent autrement que par réinjection continue, que ce soit à quartz, à couplage capacitif ou à AOP.
Même les oscillateurs sinusoïdaux RC travaillent sans se soucier de l'état de charge des condos.

Dans le schéma que j'ai donné, il n'y a pas besoin de faire intervenir le bruit blanc pour expliquer le démarrage de l'oscillation, les conditions de départ sont suffisantes.

[stefjm]

Parce que le montage est à base d'automatique et que c'est fait pour...