Calcul du diamètre de la terre

[triall]

@ansset , exact , mes triangles ne sont pas semblables, je suis allé trop vite ...
-----

[Rachilou]

oui et non.
tu peux faire une approche théorique mais qui ne fonctionnera pas.
au coucher du soleil , les rayons sont légèrement "déformés" par la gravitation terrestre.
( le soleil est encore visible alors qu'il est déjà "sous" la terre ).

Bonjour Anset...

Ce qui compte c'est la variation de la mesure.
S'il y a un défaut sur la 1ere mesure, alors il y aura aussi un défaut sur la 2e mesure.
Le décalage sera reporté, et en valeur absolue, nous aurons la même chose.
Sauf erreur de ma part.

[Rachilou]

Bonjour à tous, merci à Rachilou de nous promener ainsi sur les plages, au coucher de soleil ..
Juste, pour le mat.. , je crois qu'il s'agit plutôt de rac(Rh) et non rac(2Rh) , en se reportant au dessin mess 14 , on a vu que les triangles AOB et ABC sont semblables , et en confondant AB et AC on a AB/R=h/AB ; AB²=Rh ..
Sinon, pour le coucher de soleil, le temps de coucher va nous donner un angle , (360°=24h) , c'est l'angle apparent du soleil , je ne vois pas la suite immédiatement !

Triall.


Connaissant la hauteur du mat et l'angle entre le haut et le bas du mat, tu peux déterminer le reste.
Ma question : comment tu procèdes pour mesure l'angle ?
Peux-tu le décrire ?
Merci d 'avance.

-------------


En ce qui concerne " le temps de coucher du soleil va nous donner un angle , (360°=24h)" c'est la bonne voie... super.


Allez je donne des indices :
Je sais que je mesure 1.75m et que la terre effectue une rotation en 24 heures.
Je suis sur une plage et relativement au soleil qui se couche je peux effectuer 2 mesures (voir croquis) qui vont me permettre moyennant des calculs de déterminer le rayon de la terre.
La précision du résultat ne tiendra que sur les mesures effectuées avec ma montre et mes yeux.

De ce que je sais, la résolution du problème s'effectuer en 2 équations.
Le résultat de la première contribue à la seconde.

[triall]

Connaissant la hauteur du mat et l'angle entre le haut et le bas du mat, tu peux déterminer le reste.
Ma question : comment tu procèdes pour mesure l'angle ?
Peux-tu le décrire ?
Merci d 'avance.

Arghh !Effectivement , compliqué pour avoir cet angle, vu que le bateau a disparu ! ..Il nous faut alors la distance du bateau !
Puis ; avant d'être encore rattrapé par la "patrouille" , 24 h n'est pas égal à 360° , sauf à l'équateur et à l'équinoxe, il doit falloir diviser par cos(latitude).cos (déclinaison )car il s'agit de hauteur (sens navigation) .A l'équinoxe , au pôle nord le temps de coucher de soleil est ..infini , cos90=0...cos0=1

Bon, avec la taille, je tente : la différence de temps va nous donner un angle,
plage.jpg
l'angle BiA sans doute, mais je me demande s'il faut tenir compte de la latitude et déclinaison, on va dire 24h=360° .
Alors, ce coup ci mes triangles ABi et OAC sont bien semblables, on démontre "facilement" que AB=CD et i milieu de AC en remarquant que les triangles rectangles AOC et OBD sont égaux.(2 angles égaux et un côté égal)

On trouve alors AC=rac(2R.AB) or alpha =AC/R alpha étant , à priori ,l'angle donné par la différence de mesure du temps entre la mesure au ras de l'eau et la mesure debout.
On a sauf erreur , R=2AB/alpha² , AB étant ma hauteur (1m75 ) , et l'angle alpha donné par la différence de temps du coucher de soleil avec sous réserve que 24h=360° ;1°=4mn

[invite51d17075]

n'oublie pas ce que j'ai mentionné plus haut.
les rayons du soleil sont "déformés" par la gravitation.
mais tu dois ( peut être ) considérer que la déformation est la même entre le début du coucher et la fin.
je n'ai pas fait le calcul.

[invitef29758b5]

les rayons du soleil sont "déformés" par la gravitation.

C' est plus que négligeable .
Les déformations dues à l' atmosphère sont bien plus importantes . De même que les défauts de sphéricité .

[triall]

n'oublie pas ce que j'ai mentionné plus haut.
les rayons du soleil sont "déformés" par la gravitation.
mais tu dois ( peut être ) considérer que la déformation est la même entre le début du coucher et la fin.
je n'ai pas fait le calcul.

Non, ansset, je l'ai indiqué plus haut , ce n'est pas la gravitation terrestre qui va notablement courber les rayons (relativité générale) , mais l'atmosphère avec effet de mirage, et comme l'indiquait Rachilou, de toutes façons l'effet se compense ..

[invite51d17075]

oui à dynamix mais non à triall. ( mea culpa )
le soleil semble très aplati quand il se couche.

[invitef29758b5]

Avec toutes ces histoires de marins , on calcule le diamètre des océans .
Après , on fait comment pour avoir le diamètre (moyen) de la terre ?

[triall]

OK, pour l’aplatissement, mais les mesures que nous propose Rachilou sont une différence de temps couché -debout, que je propose de transformer en angle , avec le calcul plus haut message 34, l'aplatissement ne devrait pas influencer les mesures ...
Si j'ai bien compris on chronomètre le coucher en position allongée au ras du sol , puis on se lève et on regarde combien de temps supplémentaire on voit encore le soleil ..

[invite51d17075]

franchement, comme je l'ai dit, je n'ai pas fait le calcul.
j'ai juste un doute sur la fiabilité du résultat.
cordialement.

[invite51d17075]

en complément, je suppose que tu veux parler de "temps" entre les deux évenements et pas d'angle.
mais celà suppose de connaitre la distance et le diamètre du soleil, qui n'est pas stable dans l'année.
( me demande si j'ai compris ton idée de calcul ? )
cordialement.

[invitef29758b5]

Finalement la méthode d' Erathostène n' était pas mauvaise .
Il lui manquait de la fiabilité dans les mesures de distances et une montre .

[invite6dffde4c]

Re.
La méthode de cet exercice n’est pas une méthode qui ait un quelconque intérêt pratique autre que celui de faire un exercice de géométrie.

Les effets de l’atmosphère ne doivent pas trop jouer car on est au même en droit et (presque) à la même hauteur.

Mais pour une mesure d’angle absolu, l’atmosphère joue énormément. On peut le voir avec l’aplatissement du soleil à l’horizon. Et, au sextant, on ne prenait jamais des étoiles plus bases que 30°. Même s’il y avait des tables pour faire les corrections.
A+

[invitef29758b5]

Re.
La méthode de cet exercice n’est pas une méthode qui ait un quelconque intérêt pratique autre que celui de faire un exercice de géométrie.

Il est quand même question d' une "assez bonne précision"
Il faut donc prendre en compte la précision de la méthode .

[triall]

en complément, je suppose que tu veux parler de "temps" entre les deux évenements et pas d'angle.
mais celà suppose de connaitre la distance et le diamètre du soleil, qui n'est pas stable dans l'année.
( me demande si j'ai compris ton idée de calcul ? )
cordialement.

On appelle ça l'angle horaire , la rotation de la Terre permet de transformer un temps en angle, si l'on se place sur un plan équatorial (comme pour un télescope ) on a 24 h=360° , mais ici il s'agit de hauteur (astronomie) , il faut sans doute diviser comme je l'indiquais par cos(latitude).cos(déclinaison du soleil ) au lieu d'avoir 1mn=0.25°(pour24h=360°) , on aurait 1mn=0.25/cos(lat)cos(dec) °.
Exemple à l'équateur, et à l'équinoxe , le soleil plonge exactement perpendiculairement dans l'eau cos (lat) =1 ; cos (dec)=1 , et passe exactement à la verticale à midi ...mais au pole nord ou sud, à la même époque , le soleil ne se couche jamais , et on ne pourra pas mesurer le rayon ...
Ceci dit , ces mesures , calculs sont théoriques, je crois,dans l'esprit de Rachilou car mesurer ça à plat ventre puis debout , avec le problème des vagues, je compte aller en Corse sous peu , j'essaierai , mais je doute que l'on puisse mesurer quoique ce soit !
Sinon, donc selon ces mesures, le diamètre du soleil n'apparait pas , il sert juste de repère ....

[invite51d17075]

pardon, mais tj pas saisi.
si tu prends le soleil comme référence, tu prends quoi comme repère par rapport au soleil.
s'il avait 2 fois sa taille, il mettrait 2 fois plus de temps à se coucher ???!!
Cdt

[invite6dffde4c]

Il est quand même question d' une "assez bonne précision"
Il faut donc prendre en compte la précision de la méthode .

Re.
Comme « assez bonne précision » ne veut rien dire (ça manque de précision), on peut mettre ce que l’on veut dedans.

Mais il est vrai que ce serait intéressant de faire un calcul d’erreur. Si Rachilou veut le faire, ce sera un bon exercice.
On peut considérer que l’on peut détecter le passage du bord supérieur ou inférieur du soleil sur l’horizon avec une seconde d’erreur.
Il faudrait calculer l’erreur suivant la différence de hauteur.

Mais actuellement toutes ce méthodes surannées n’ont d’autre intérêt que l’intérêt historique (que j’aime) et celui de la géométrie (que j’aime aussi, amis qui n’est plus enseignée).
A+

[Rachilou]

Bravo Triall.

On part aussi du principe que dans l'idéal on devrait se trouver sur l'équateur et à l'équinoxe.
Mais comme c'est un exercice de géométrie on passera outre.

On mesure le sommet du soleil ( au point de sa disparition à son couché) au Temps 0 en position allongée.
Je me lève et je recommence. Temps 1 en position debout pour une visée à partir d'une hauteur d'1m70 (je mesure 1.80m mais j'enlève 0.1m)
Peu importe que le soleil soit bien rond ou aplati. Bien sur avec des jumelles la mesure serait plus précise.
Les deux lignes de mes visées sont tangentielles à la circonférence de la terre, donc je peux leur associer un rayon de la terre qui formera un triangle rectangle (voir dessin).

Il faut compter environ 10 secondes entre T0 et T1 (entre la position allongée et debout) pour une personne d'1m80
De là, je détermine l'angle qu'a effectué la rotation de la terre pendant ces 10 secondes, car quel que soit le diamètre de la terre, si elle tourne de 360° en 24 heures, alors en 10 secondes elle tournera d'une fraction proportionnelle à ces 360°:

1) (360° * 10s) / (24h* 3600s) = 0.04166°

Avec la fonction cosinus on détermine directement le diamètre de la terre.

2) r / (r+h) = cos (alpha)

avec :
cos (alpha) = 0.9999997356
r = diamètre de la terre
h = 1.70m ( hauteur de visé )

Pour tomber sur le rayon exacte de la terre, la mesure précise de T1-TO devrait s'effectuer au millième de seconde (10.032 secondes ) soit cos (alpha) = 0.9999997331


Crdt.

[Boumako]

Bonjour

Si la montre a une certaine valeur on peut aussi l'utiliser en guise de paiement pour soutirer la réponse à un cartographe compétent.

[triall]

OK, Rachilou, "ma formule" R=2h/alpha² est bonne aussi, elle donne rayon=6400 km...pour 10secondes ...Mais le cos est plus rapide effectivement...
Je me pose toujours la question de savoir s'il faut tenir compte de la latitude du lieu et de la déclinaison du soleil .En ce cas ce n'est pas bien plus compliqué, je suis pratiquement certain qu'il faut diviser le temps(10s ici) par cos(latitude)xcos(déclinaison) .Il faut retrouver la formule de la hauteur (sens astronomique) du soleil .Quand je faisais des cadrans solaires de précision, je l'avais trouvé cette formule ...
@ansset , le temps de coucher du soleil ne compte pas, c'est le temps supplémentaire de vue lorsqu'on est debout , la visée est donc le haut du soleil , son diamètre ne joue pas .

[invite51d17075]

OK triall, je n'avais juste pas saisi ton mode de calcul.

[triall]

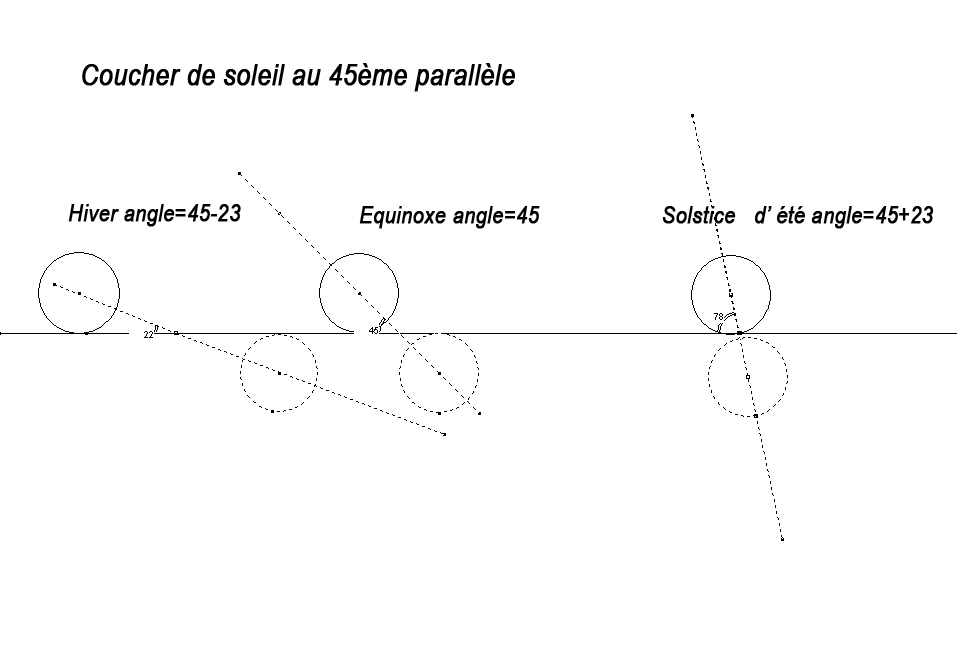
Sauf grosse connerie , voilà selon moi, comment se passe un coucher de soleil au 45ème parallèle , par exemple , suivant la saison .
A l'équinoxe, le soleil "plonge" avec un angle de 45°
On voit que l'hiver les couchers sont interminables , l'été plus rapides, et au vue du dessin, le temps serait plutôt alors divisé par cos(latitude +déclinaison) ; mais je ne sais toujours si dans les mesures de Rachilou la latitude et la déclinaison entrent en jeu ...

[invite6dffde4c]

Re.
C’est correct.
À l’équinoxe, aux pôles, le soleil fait le tour de l’horizon visible partiellement.
Et dans les tropiques, le coucher du soleil est très rapide (deux minutes entre le bas et le haut).
A+

[Rachilou]

Re.
Comme « assez bonne précision » ne veut rien dire (ça manque de précision), on peut mettre ce que l’on veut dedans.

Mais il est vrai que ce serait intéressant de faire un calcul d’erreur. Si Rachilou veut le faire, ce sera un bon exercice.
On peut considérer que l’on peut détecter le passage du bord supérieur ou inférieur du soleil sur l’horizon avec une seconde d’erreur.
Il faudrait calculer l’erreur suivant la différence de hauteur.

Mais actuellement toutes ce méthodes surannées n’ont d’autre intérêt que l’intérêt historique (que j’aime) et celui de la géométrie (que j’aime aussi, amis qui n’est plus enseignée).
A+

Bonsoir.

Pour 10,032 secondes je suis pratiquement à 6370km de rayon (rayon réel de la terre)
Si je fais une erreur d'1 seconde, par exemple je note 11 secondes alors la valeur chute sacrément : 5314km de rayon soit 0.83% de la valeur reconnue.


Crdt.

[invite51d17075]

j'ai pas un chrono qui fasse ça !
mais ça existe
Cdt

[invite6dffde4c]

Bonsoir.

Pour 10,032 secondes je suis pratiquement à 6370km de rayon (rayon réel de la terre)
Si je fais une erreur d'1 seconde, par exemple je note 11 secondes alors la valeur chute sacrément : 5314km de rayon soit 0.83% de la valeur reconnue.


Crdt.

Bonjour.
Comme je l’ai déjà dit, le seul intérêt de cet exercice est de vous faire réfléchir et travailler. Pas d’établir une nouvelle valeur plus précise du diamètre de la terre.
Mais vous pouvez améliorer la précision si vous augmentez la hauteur et donc, le temps entre les deux couchers de soleil.
Si vous avez du mal à monter les étages, vous pouvez faire la manip au lever de soleil en commençant par la mesure en hauteur.
Au revoir.

[triall]

Bonjour, après réflexion , le fait de prendre de la hauteur quand le soleil s'est couché , le fait "réapparaitre"; et ensuite il "replonge" , avec l'angle que j'ai indiqué au message 53 , c'est à dire latitude + déclinaison (qui varie de + 23 à -23 °sur l'année) .A ce moment du coucher la hauteur (angle vertical que fait l'astre avec l'horizontale, je me comprends! )du soleil est nulle ; et j'avais remarqué cet angle de plongée, en l 'observant chez moi .Je n'ai pas la mer , mais les Alpes sont à une vingtaine de km ..
Donc le soleil plongeant de biais avec cet angle, il faut(doit falloir) diviser par cos(latitude+déclinaison )le temps supplémentaire trouvé .Les immeubles de Monaco me semblent bien disposés pour un calcul !
J'avais calculé cette rotondité (le rayon terrestre )en notant la différence entre le lever officiel (hauteur du soleil =0°) et l'heure effective à cause des Alpes , et de leur altitude(ayant la formule de la hauteur en fonction de l'angle horaire , latitude et déclinaison) ....C'est un peu la même chose que ce que propose Rachilou...

[invitef29758b5]

Mais il est vrai que ce serait intéressant de faire un calcul d’erreur

En partant de la formule de triall (qui est juste en pratique et peut se déduire de celle de Rachilou) :
L' erreur relative sur le rayon est égale à l' erreur relative sur la hauteur et au double de celle sur le temps .

[invite7d411dcd]

[EDIT : ] Tout ça a déjà été dit en fait, j'ai zappé des pages... My bad ![/EDIT]

Yo !

Tu peux aussi mettre un clampin sur une échelle (assez grande...), et l'autre clampin en bas de l'échelle. Pas besoin d'aller chez le voisin à l'ouest et de téléphone !
Sinon, si ta maison à des étages, tu peux faire la mesure au rdc et au deuxième.

Je vous dis combien je trouve ce soir ! (A bah zut, il y a pas de soleil là où je suis...)