Calcul d'une force discontinue .

[triall]

Bonjour à tous , j'ouvre un post nouveau car je ne veux pas polluer le post "Effet de la force sans contact de matière" .
J'ai été étonné de la réaction de Coussin et de Dynamix sur le calcul de la force forcément discontinue qu'exerce , en rebondissant, une ou plusieurs billes sur une boîte .
La bille de masse m est dans une boîte hermétique, et rebondit sans arrêt de manière élastique .

Un autre exemple, avec un fusil mitrailleur on bombarde un écran avec des balles de masse m à une certaine fréquence n , exemple n=10 10balles par seconde .
Avec ces 2 exemples, on voit que si le rebond de la bille est lent (faible fréquence) on peut difficilement parler de force sur le plancher de la boîte ; et pourtant , il est "évident" qu'au final la bille communique son poids à la boîte . Si la bille rebondit avec une fréquence assez élevé (elle tombe d'une petite hauteur) , la force peut alors être mesurée avec une balance , d'autant plus s'il y a plusieurs billes .
On doit évidemment comparer cet exemple à du gaz enfermé dans une boîte , le gaz frappe le plancher et le plafond, et la différence de la force de pression entre le plancher et le plafond ...donne au final le poids du gaz . Les molécules, malgré leurs rebonds incessants les unes contre les autres possèdent au final plus de vitesse sur le plancher que sur le plafond, à cause de la pesanteur .
Je prétends que et pour la bille qui rebondit, et pour le mitraillage la force "moyenne" F=(mv-mv')xf , m était la masse de la bille ou balle v, vitesse (vecteur) juste avant le choc , v' vitesse juste après le choc , f fréquence des tirs ou des rebonds .
Je vais prendre une troisième exemple pour expliquer le calcul .
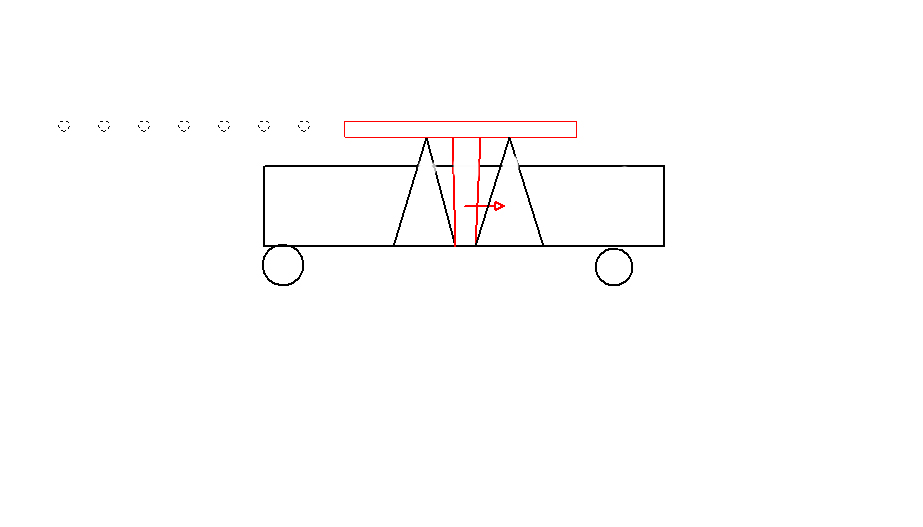
Il s'agit d'un engin à réaction qui envoie des balles vers l'arrière, et de ce fait avance .Désolé pour le dessin.


On comprends de suite que l'équation du mouvement n'est pas linéaire, l'engin avance par à coups, en prenant une petite vitesse à chaque fois , mais cela lui procure en moyenne une accélération .
Il est admis que la force de poussée en ce cas =masse éjectée par seconde x vitesse d'éjection . Newton avec le principe de la conservation de mouvement dit qu'à chaque tir , l'engin prend mv comme quantité de mouvement , ainsi selon ma formule plus haut F=mvxf , c'est exactement la même que" la force de poussée en ce cas =masse éjectée par seconde x vitesse d'éjection "
En effet masse éjectée par seconde = masse éjectée x fréquence des jets !
Ainsi "mon" équation fonctionne ici .
En fait on a F.t=delta .mv F étant la force appliquée à m pendant le temps t , cela provoque une variation de la quantité de mouvement delta .mv . Cela revient à dire que la force est linéaire pendant le temps t , période de tir , le résultat est le même . On a donc F=delta.mv/t mais attention t est la période des tirs!
Je reviens donc à ma bille de masse m qui rebondit dans la boîte .
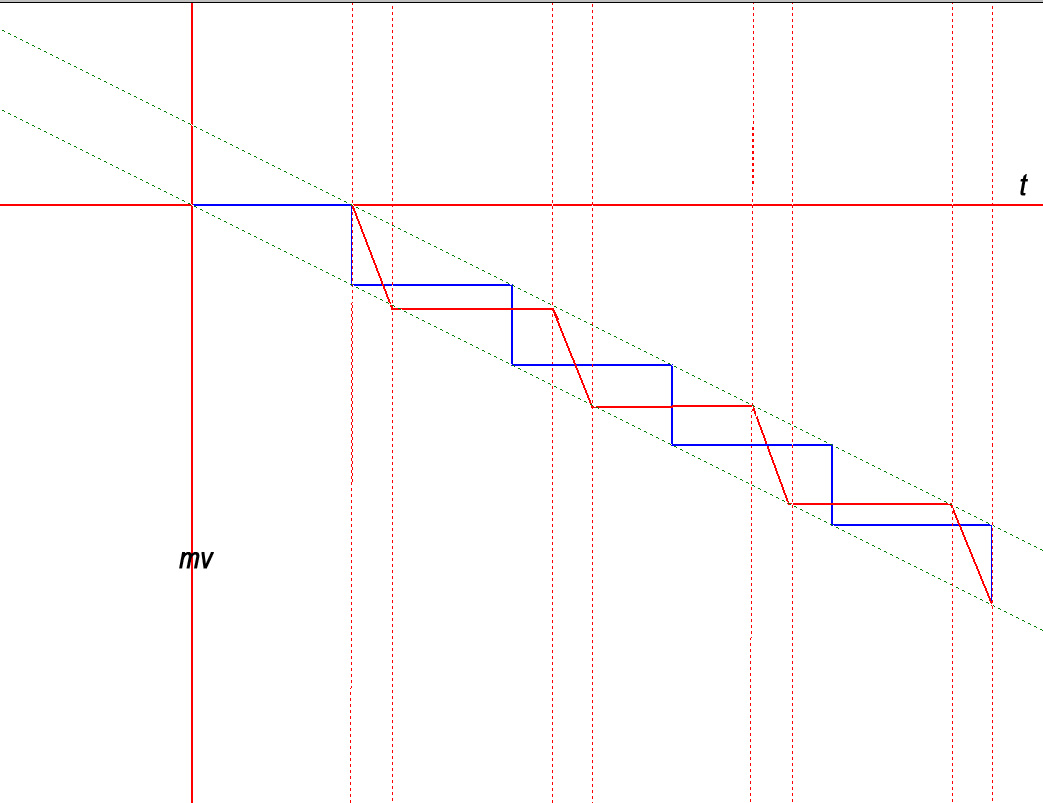
Je vais calculer la force qu'exerce la bille sur le plancher , en supposant le choc élastique . A chaque rebond , la bille cède 2mv au plancher selon les chocs élastiques .
Alors F=2mv/t : t étant la période des chocs, donc le temps mis d'un aller retour !v la vitesse lors du choc , on sait que v=g(t/2) , car le temps de tomber est bien de t/2 t étant la période toujours ..
Il vient de suite, ô miracle F=2mgt/2t =mg , la force calculée ainsi est bien le poids de la bille . "Mon" équation marche encore ici , elle est très valable cette équation , je crois. Coussin et Dynamix pensent qu'elle est fausse , qu'ils me donnent alors" leur" expression de la force moyenne de tous ces chocs ! Je n'ai pas du tout leur niveau par ailleurs, je le sais; mais il me semble que mon raisonnement sauf coquille est correct ici!
A débattre si vous le voulez !
Merci de vos remarques
-----

[triall]

Pour dynamix et coussin, notamment qui devraient indiquer ," s'il leur plait" , s'il persistent à dire que mon équation est fausse !
Rebonjour, mon explication ci dessus est un peu laborieuse , mais bonne , je pense.
J'essaie de la résumer mieux .
Je reprends l'exemple des balles tirées sur un écran , ce mitraillage provoque une force que je suppose constante , et non en dent de scie avec force énorme, pas de force, force énorme-pas de force... ,Cette supposition , qui ne modifie pas les grandeurs finales ,donne donc une accélération constante, et une vitesse linéaire de la forme v=gamma.t et je peux écrire alors F=m.delta.v/delta.t =(mv-mv')/(t-t') ; t-t' étant le temps en 2 impacts, donc la période du mitraillage, v étant la vitesse juste avant le choc, v' juste après . D'où F=(mv-mv')/période=(mv-mv')xfréquence des tirs .
F est donc la force moyenne cédée à l'écran par les balles qui est égale , et de sens contraire à la force donnée aux balles par l'écran !
Est-ce plus clair ?
Bonne journée

[Dynamix]

Merci mon cher Triall de m' inviter dans cette discutions .
Il me semble que tu as fait tienne la devise "pourquoi faire simple quand on peut faire complique" et que tu l' applique un peu trop à la lettre .
Bref , le point de départ était :

Bonsoir, personnellement j'ai toujours vu une force comme un "échange de quantité de mouvement", car c'est bien des mv/seconde de la quantité de mouvement par seconde . Si l'on veut avoir une action à distance sur un objet on peut lui envoyer des cailloux, qui vont lui donner de la quantité de mouvement ...

Le fait qu' en dynamique une force est égale à une variation de quantité de mouvement n' implique pas qu' à toute force est associée une quantité de mouvement .
Bien sur si tu en cherche une , tu en trouveras une , quitte à couper les cheveux en 2^N (il suffit de faire tendre N vers l' infini )

D' après ton explication , le poids du gaz se transmet par l' agitation moléculaire , il devrait donc être fonction de cette agitation . Et si on la ralentie ? Et si à la limite on la stoppe ? La boite s' envole ?
Non , le poids est indépendant des mouvement à l' intérieure de la boite .

N' est il pas bien plus simple et de plus facilement quantifiable d' expliquer cela comme le principe d' Archimède ? La pression étant à l' intérieure on a juste à inverser le vecteur dS , ce qui fait que la poussée est de haut en bas .

L' exemple de la mitrailleuse ne convient pas vu qu' il y a apport permanent d' énergie , ce qui n' est pas le cas dans la boite .

[triall]

D' après ton explication , le poids du gaz se transmet par l' agitation moléculaire , il devrait donc être fonction de cette agitation . Et si on la ralentie ? Et si à la limite on la stoppe ? La boite s' envole ?
Non , le poids est indépendant des mouvement à l' intérieure de la boite

En tous cas , mon équation est bonne, je suis certain que vous n'avez pas compris la démarche ; il s'agit de lisser une force qui est périodique et discontinue .
J'ai montré , justement que cette force ne dépend pas de la hauteur h à laquelle tombe la bille .Si on ralentit l'agitation, cela ne change pas la force , si l'agitation s'annule, les molécules ou la bille reposent sur le plancher par contact et donnent leur poids au plancher ..
Rappel j'écris, comme je suppose la force constante pendant le temps t de la période :F=m delta (v)/t avec delta.v = 2v , car la vitesse v passe de v à -v , le delta est 2v .Si vous préférez F=(mv-mv')/delta .t ; avec v'=-v , je répète, on fait comme si la vitesse augmentait linéairement en fonction de t , pendant ce temps aller-retour .
Exemple , si on laisse tomber la bille d'une petite hauteur , la période du rebond va diminuer , la vitesse aussi , au final c'est la même force mg .
J'ai aussi fait le calcul avec h=0.5gt² , v= rac(2gh) , on calcule le temps d'un aller retour t=2xrac(2gh) ; F= 2mv.xt=mg , vous ne voulez pas voir cette égalité dirait -on . La hauteur h a disparu , vous devez le remarquer !
Le résultat est que la force calculée ainsi est lissée, on suppose que la force est constante pendant l'aller retour , ce qui est presque le cas avec un grand nombre de billes .
Sinon, à la limite, avec seulement quelques molécules de gaz , le poids donné aux parois (plancher - plafond) est erratique , mais donne au final un poids moyen nmg des n molécules présentes...

La poussée d'un réacteur F=masse éjectée par seconde x vitesse d'éjection est absolument identique regardez bien , et imaginez comme le dessin ci dessus que le réacteur éjecte ses molécules une à une ! , chaque molécule donne mv , la Force est F= delta.mv/t =mv/t(les molécules passent de 0 à v) 1/t étant le nombre de molécules qui sortent par seconde , t étant la période d'éjection , le temps entre 2 jets.......

[A voir en vidéo sur Futura]

[coussin]

J'ai déjà dit tout ce que j'avais à dire sur votre démarche.

Juste, sur ce point:

J'ai montré , justement que cette force ne dépend pas de la hauteur h à laquelle tombe la bille

La raison pour laquelle votre force ne dépend pas de la hauteur h est parce que vous avez considéré une bille et une paroi parfaitement indéformables, donc le choc s'effectue en un temps nul, la vitesse de la bille est exactement discontinue, la force est donc infinie qu'elle que soit la hauteur de chute.

Reprenez votre raisonnement avec une balle de tennis, déformable. Et voyons ce que vous trouvez...

[triall]

Bonjour, coussin, je trouverais sans aucun doute mg , surtout quand la balle de tennis aura fini de rebondir ...
Il est évident que la balle "donne" son poids à la boîte lors d'un rebond , quel qu'il soit , elle ne peut le faire en "vol" !!
Je ne sais pas faire ce calcul d'amortissement de suite(une piste ?), mais il est évident que pour des molécules, par exemple lorsqu'on les refroidit, leur poids ne diminue pas . A l'inverse si l'on donne une vitesse initiale supplémentaire(augmentation de température) aux billes (molécules) , cette vitesse initiale va se retrouver en bas , et en haut ensuite avec la même valeur (opposée) , et donc s'annuler .La pression n'augmente pas le poids qui est donc, j'en suis certain , la différence des 2 forces qu'exercent les molécules(billes) sur le plafond d'une part et le plancher d'autre part.. Force plus importante sur la plancher .Pour un gaz on peut estimer que les molécules tombent , et rebondissent de la hauteur de leur "libre parcours moyen" .
Le poids du gaz contenu dans une enceinte hermétique est bien égale à la différence des forces de pression exercées d'une part sur le plafond , et d'autre part sur le plancher ..
C'est effectivement l'inverse pour la poussée d'Archimède , mais cette dernière égale au poids du volume extérieur de gaz ou de fluide que contient la boîte (volume déplacé de fluide) , ..Pour la résultante, on ajoute le poids et la poussée (avec leur signe) .
Je vous invite à bien lire l'équation de la poussée d'un réacteur ,(Poussée=masse éjectée par seconde x vitesse d'éjection) en faisant fortement diminuer la masse , jusqu'à éjecter les particules une à une , vous verrez que c'est exactement l'équation et la démarche que je propose .
Bonne journée

[coussin]

Voilà comment je vois la situation. Je considère une bille de masse mb, vitesse vb qui tombe en chute libre sur une plaque de masse mp, vitesse vp. Je me place dans le référentiel du centre de masse des deux objets.
J'étudie la quantité de mouvement de la bille et de la plaque en fonction du temps.
Je considère que le choc dure t_choc (si vous considérez des objets indéformables, ce t_choc sera nul).

De O à A on a la phase de chute libre. Le point A est donc à t=sqrt(2h/g) et la vitesse de la bille à ce point est sqrt(2gh).
Pendant le choc, on a le principe d'action-réaction de Newton avec la force exercée par la plaque sur la bille F_p->b et la force exercée par la bille sur la plaque F_b->p qui est égale et opposée (les flèches bleues).
Au point C, la bille est revenue à son point de départ à la hauteur h et tout recommence.

Ce que vous calculez est, finalement, la pente de la partie OA qui est -mg effectivement… Mais rien à voir avec
(i) la quantité de mouvement transmise à la plaque (qui est la différence de quantité de mouvement entre les points A et B)
(ii) la force exercée sur la plaque qui est la pente de la partie entre A et B (les flèches bleues).

Pièce jointe supprimée

Qu'en pensez-vous ?

[JPL]

Toutes les images (photos, schémas...) doivent être postées dans un format graphique (gif, png, jpg). Merci.

[coussin]

Je re-poste ma PJ

[triall]

Bonjour, effectivement c'est tout à fait ça dans la réalité, mais attention, évidemment la pente OA représente -mg, car il s'agit de la force de pesanteur, la vraie, qui fait tomber (accélérer) la bille , ou la freine pendant la montée , elle devrait aussi apparaître pendant le choc ..
Effectivement je considère le choc élastique , et donc le temps de choc = 0
Si l'objet repose sur une balance qui représente la Terre , de masse M , de vitesse V , la bille de masse m et de vitesse v , à tous moment on a mv=MV , je considère alors que la Terre passe de V à-V de manière linéaire pendant toute la durée de l'aller retour .
On a alors un calcul moyen de la force F=delta MV/delta t =deltamv/ t où t est la période , on trouve F=mg (voir 2 calculs différents, plus haut) ; mais ce n'est pas mg la force de gravité (qui est est vraiment linéaire ) , c'est la force de réaction du support, ou la force exercée par les chocs ....

Cette force de réaction DOIT évidemment être égale à mg ou nmg dans le cas de plusieurs billes , même si elles rebondissent au plafond, je l'ai montré !!! On en déduit que tout se passe comme si le temps de choc était nul, et que la force était constante pendant les chocs successifs, alors qu'en réalité la force a des "à coup" , est discontinue .
Alors vous allez me dire que l'on DOIT inclure ce temps t de choc , mais
1/ On ne le connait pas , ni la force exercée pendant ce choc .par contre si F est cette force , on sait que (F-mg).t=2mv , j'ajoute - mg car pendant le choc, la gravité joue aussi !!!
2/De toute façons, la moyenne de la force DOIT être égale à mg , c'est par le plancher que la bille donne sa force moyenne qui ne doit pas être différente lors d 'un arrêt éventuel des rebonds ...
3/Si l'on arrivait tout de même à faire un calcul de la moyenne de la force précis des rebonds on DOIT(est obligé) de trouver mg .Comme il y a en réalité un temps de rebond, il faut aussi rallonger h , étudier ce qu'il se passe exactement .. mais , le résultat est obligatoirement mg , il n' y a pas d'autre solution , c'est une réalité connue , les chocs successifs des molécules donne leur poids , le communique à la balance , mais en toute rigueur , cette force est discontinue, même avec un très grand nombre de molécules .
Pour la poussée d'un réacteur, je le répète , c'est le même calcul, on ne se soucie pas du temps d'éjection des molécules, non ?
Sujet intéressant , je trouve.
Bonne journée.

[coussin]

elle devrait aussi apparaître pendant le choc ..

Non, rien à voir. Cette force, si je la prend constante par commodité comme j'ai fait, consiste à transférer 2mb*sqrt(2gh) en un temps t_choc. Je répète, encore une fois, que si t_choc est nul cette force est infinie. Dans la pratique, vous vous rendez bien compte que t_choc est bien bien plus petit que le temps de chute (suffit de regarder une bille rebondir…). Cette force sera bien plus grande que mg.

J'ai expliqué, je crois, en détail mon point de vue. Je pense que l'on va alors accepter de ne pas être d'accord et puis c'est tout

[coussin]

Deux exemples me viennent avec lesquels vous vous rendrez peut-être compte que vous avez tord: pour vous, il n'y a aucune différence entre se tenir sur une balance ou se laisser tomber sur une balance. Celle-ci indiquera toujours 80 kg. Prenez une bille en acier. N'y a-t-il pour vous aucune différence entre poser cette bille sur une vitre et laisser tomber cette même bille sur cette vitre d'une hauteur, disons, de 2m. Je vous invite à faire l'expérience si vous ne tenez pas trop à votre vitre...

[coussin]

Je termine en signalant qu'en prenant (proprement...) la limite de hauteur de chute h ->0 du formalisme que j'ai présenté, on retrouve une force égale à mg transmise à la plaque (avec en prime une introduction aux états quantiques gravitationnels; faut proprement réfléchir à ce que ça veut dire que la bille repose sur la plaque, au niveau microscopique)

[triall]

J'entends bien vos arguments, mais vous ne voulez pas entendre que cette force moyenne sera et doit être mg , ou si vous préférez l'accélération moyenne de cette force sur la balance sera g sur un grand nombre de rebonds ..
Il n'y a aucune raison pour que la force soit mg lorsque h> o , et plus petit pour h plus grand . mais on a de même mg lorsque temps de choc >0 .
C'est le cas quand on refroidit un gaz , le libre parcours moyen (h ) est plus grand , mais le poids ne varie pas ..
J'ai l'impression que vous ne voulez pas comprendre que ces chocs communiquent une force de haut en bas = au poids total des molécules .
Je ne sais pas exactement comment les molécules se débrouillent, mais au final , quand une boîte hermétique est sur une balance, le poids indiqué sur la balance est bien celui du gaz (de la totalité des molécules de gaz) +celui de la boîte -poussée d'Archimède si on veut , mais comme il se doit on peut supposer le vide autour ...
Si l'on prend en compte un temps t de choc, donc un aplatissement de la bille-molécule , le calcul de t ne sera plus le même , je ne suis pas sûr que la quantité de mouvement soit conservé, par exemple pendant l'amortissement, étant donné que le poids "travaille" ..
Donc, oui, je maintiens,pour la balance , ce sera pareil si les molécules sont à l'arrêt sur le plancher , ou si elles rebondissent d'accord ou pas ? En tous cas c'est ce que l'on constate , mais évidemment il faut un grand nombre de molécules ou de billes .
Le poids du gaz sur la balance est bien du aux chocs des molécules , non ?
Votre exemple du bris de glace est très déloyal , vous le savez , on a quelques g pendant le choc bref , et une très grande force .

[coussin]

Votre exemple du bris de glace est très déloyal , vous le savez , on a quelques g pendant le choc bref , et une très grande force .

Oui, c'est ce que je me tue à vous dire. Et vous, vous persistez à dire que non, on a pas une très grande force mais seulement le poids mg.
Je me demande maintenant si vous ne vous moquez pas de moi...

[Dynamix]

Le poids du gaz sur la balance est bien du aux chocs des molécules , non ?

Cette formulation induit en erreur .
Je pense que l' idée est que "le poids du gaz est transmis à la boite par les chocs des molécules" .
C' est une idée tortueuse , invérifiable et non quantifiable .
D' autant plus que le poids mesuré par la balance est indépendant de ce qui se passe dans la boite .

[stefjm]

Bonjour,
Je n'ai pas tout lu et je n'ai pas le temps de détailler.

J'ai l'impression qu'il suffit d'un dirac pour modéliser votre choc.
Amplitude infini pendant temps nul, mais énergie finie.

Cordialement.

[triall]

Bonjour, dynamix pour un fluide comme l'eau , le poids indiqué par la balance est bien Mg , le poids des molécules , c'est la même chose pour un gaz , et très vérifiable (balance, Bolztmann ,théorie cinétique des gaz) . Le poids des molécules (eau gaz ou solide)est bel et bien transmis par les chocs, par quoi voulez-vous qu'il soit transmis d'autre ?
Je reviens donc sur le dessin 1 . message 9 de coussin .
On voit clairement que si l'on prends un temps t de choc non nul, la courbe moyenne ne peut prendre une pente de mg , sauf si ...
la molécule repart en moyenne plus vite qu'elle est venue !
Ne criez pas tout de suite , c'est une hypothèse très plausible !
Les molécules ont une énergie interne ,rapport à leur température, en cèdent une partie au support , en récupèrent .....
Elles sont comme un ressort qui vibre à une certaine fréquence, ainsi que le support .
En rebondissant , elles "re" prennent une partie de cette énergie , ainsi elles arrivent à v sur le support et repartent à -v+ gagnant ainsi non pas 2mv , mais 2mv+ au signe près; la courbe OA de coussin est alors infléchie vers le bas , et la moyenne de la force devient bien mg , ce qui est "obligatoire".
Ci dessous la courbe bleue avec t choc =0 , et 2mv de donné à chaque fois , en rouge, t de choc non nul, mais la courbe rouge prend plus de 2 mv , les 2 courbes ont une pente "moyenne" identique (pointillé vert)

Évidemment ce processus atteint un état d'équilibre thermique, je ne saurais le décrire en détail , mais je ne vois que ceci .
Imaginez par exemple un haut parleur plat qui vibre , des billes posées dessus rebondiraient sans cesse .Si la période de vibration est petite devant le temps du choc, les molécules billes se prennent une "pichenette" vers le haut , et repartent plus vite qu'elle ne sont arrivés , de v à -v+ , empruntant de l'énergie au support, qu'elles rendent ensuite .....(équilibre thermodynamique...)
Bonne journée

[coussin]

[…]mais je ne vois que ceci.[…]

Oui enfin… Y a toujours la possibilité que vous ayez tord aussi

[Dynamix]

Le poids des molécules (eau gaz ou solide)est bel et bien transmis par les chocs, par quoi voulez-vous qu'il soit transmis d'autre ?

Vu qu' il se transmet en l' absence de chocs , c' est qu' y a bien quelque chose d' autre .

[triall]

@dynamix , le poids ne se transmet pas à la balance en l'absence de choc, quand les molécules sont en "vol" , le poids est transmis lors du choc ou interraction !
Une petite expérience : 1/pesez cette boîte
/Pesez la boîte vide
La différence notée sur la balance est le poids du gaz , poids transmis pendant les chocs , ou contact avec un gaz à 0°K qui se retrouve au fond ;ou contact dans le cas de l'eau ..
Dans le cas d'un gaz on a Pression plancher-pression plafond= rhô g h , h hauteur plafond plancher , Force = pression x surface=rhô .g h.s =
=rhô.g.Volume =Mg !(rhô.Volume = Masse )
Dîtes le lui à dynamix, après on pourra discuter de la thermalisation des molécules ou pas ...