Bonjour à tous,
Je vais essayer de vous expliquer en quelques mots mon problème, mais n'hésitez pas à demander plus d'informations si cela n'est pas clair.
Une bande d'un matériau assimilable à du caoutchouc dur est placé autour de 2 cylindres (pour avoir un ordre d'idées, bande de caoutchouc de 5 m de développé et de 2 m de largeur). Je cherche à calculer les différentes contraintes qui sont présentes dans la bande en caoutchouc, localisées ou non, pour pouvoir prédire les zones à risque (déchirures, etc.) et essayer de les simuler.
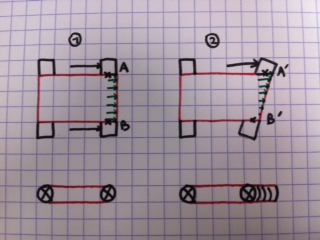
Vous pouvez trouver un croquis explicatif ici : (je n'ai pas réussi à mettre la photo dans le message... voilà, c'est fait.)
Premier cas : on applique une force avec 2 vérins sur le cylindre de droite (diamètre 8 cm, 6 bars). Force totale des 2 vérins : 6 kN. On arrive donc à une "force" répartie sur les 2 m de 3 kN/m. Etant donné qu'on applique la tension sur le produit en haut et en bas (2 "brins"), je trouve une force maxi sur le produit de 1.5 kN/m, qui est finalement présente dans l'ensemble du produit (ou en tous cas, sur la surface caoutchouc qui n'est pas en contact avec les cylindres). Si la bande de caoutchouc, après un test de traction, résiste à une force supérieure à 1.5 kN/m, on peut donc en déduire qu'elle résistera au montage. Est-ce que mon raisonnement parait correct ? Ou y-a-t-il d'autres paramètres que je n'ai pas pris en compte ?
Deuxième cas : on applique une force avec 1 vérin sur un côté du cylindre de droite. Force du vérin : 6 kN (donc 2 fois plus puissant que pour le cas 1). On arrive donc à une force répartie linéairement sur les 2 m, mais avec la force maxi là ou la bande est tendue (point A') et une force nulle là où le feutre n'est pas tendu (point B'). Comment puis-je calculer la force au point A' ? (j'imagine que l'aire des "flèches vertes" sur le dessin est la même dans le cas 1 que dans le cas 2, et donc que la force au point A' serait donc le double de la force au point A, soit 1.5 kN/m (sur un point localisé) ? Est-ce que ça parait cohérent ? Question subsidiaire, est-ce qu'il faudrait tenir compte du moment ? En effet, si on considère le segment A'B' comme un bras de levier, on se retrouve avec un moment au point B' de F*d = 6 kN * 2 m, alors qu'il n'y en aurait pas au point A'. Est-ce qu'il y a effectivement un moment sur la bande dans ce cas là ? Si oui, que pourrais-je utiliser pour le calculer, afin de pouvoir tester avec un dynamomètre si la bande résisterait à ces conditions ? Y aurait-il plus de contraintes au point A' ou au point B' ?
Je vous remercie d'avance si vous avez des pistes de réponse, les calculs mécaniques sont un peu loin pour moi, et ce cas est pour moi beaucoup plus compliqué que les cas théoriques que j'ai eu l'occasion de traiter dans ma vie (ex : poutre encastrée...). Je n'attends pas forcément de réponse définitive, mais des idées, des pistes de réflexion, et surtout votre avis sur ce problème...
Cordialement,
Pierre.
-----