Travail d'une force stationnaire

[CZ48]

Bonjour,

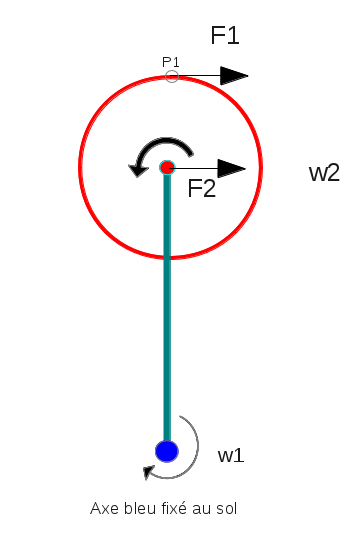
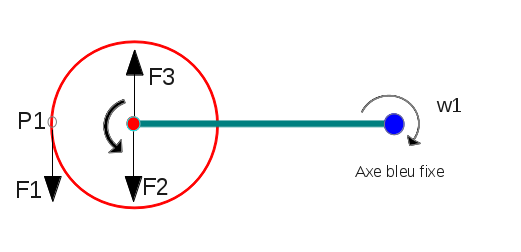
Un bras de longueur 'd' tourne à la vitesse w1 (référentiel labo) dans le sens horaire. Un disque de rayon 'r' au bout de ce bras tourne sur lui-même dans le sens trigo. Le disque est à la vitesse w2 (référentiel labo) de telle manière qu'au point P1 la vitesse linéaire soit nulle. On doit donc avoir w1(d+r)−rw2′=0, soit w2′=w1(d+r)/r. Avec w2' la vitesse de rotation du disque dans le référentiel bras. J'applique pendant un temps très court une force externe F1 sur le disque au point P1, cela ne nécessite pas d'énergie puisque la vitesse au point P1 est nulle. La force F1 applique une force F2 sur le bras. Le bras travaille de B=Fdtw1, avec F la valeur de la force F1.



Le disque perd une énergie:

1/ Soit −Frtw2′=−Ftw1(d+r), dans ce cas la somme de l'énergie n'est pas nulle
2/ Soit −Frtw2=−Fdtw1 et dans ce cas la somme de l'énergie est nulle.

Rq: Pour moi c'est le cas 1/ puisque si w1 > w2, l'énergie du bras est de Fdtw1, l'énergie nécessaire à l'application de la force F1 est de Ft( w1(d+r)−rw2′ ), donc pour avoir une somme nulle il faut bien que le disque travaille de −Frtw2′. Idem avec w2 > w1.

Comme je me doute bien la réponse est 2/ mais je ne comprends pas pourquoi dans le sens physique (qualitativement) et pourquoi dans la remarque j'ai bien w2'. Si vous pouvez m'expliquez SVP ?

A+
-----

[Dynamix]

Salut

Le disque est à la vitesse w2 (référentiel labo) de telle manière qu'au point P1 la vitesse linéaire soit nulle.

Laisse tomber c' est impossible .
Dessine ta figure quand le bras a tourné un peu et tu verras que le point P1 ne peut pas rester au même endroit

La prochaine fois (c' est toutes les semaines , il me semble) nomme tes axes , ce sera plus simple que "le bleu" , "le rouge" ...
Et ne dessine pas ta figure en position départ . Met un angle à ton bras et à ton disque .

PS une force stationnaire , ça ne travaille pas .

[CZ48]

Bonjour,

Si le temps est très court (vraiment court) le point P1 ne bouge pas pour moi ou peut être juste un poil sur le rayon mais c'est perpendiculaire à la force. Voici une image, même si j'imagine l'angle encore plus petit:



J'aimerai bien savoir pourquoi d'une manière générale la force F1 donne un couple au disque avec la vitesse w2 et non w2' si à chaque instant elle est comme je l'ai dessiné, cela suppose un système qui est capable d'appliquer la force F1 sur un dt et qui change son origine très souvent ? Si la force F1 ne travaille pas, c'est bien sur w2 que le couple doit s'appliquer.

A+

[CZ48]

Re,

J'ai fait un agrandissement, et comme je le pensais la somme des déplacements d1 et d2 donne un faible déplacement uniquement sur le rayon:



Sinon, le raisonnement est peut être le suivant:

1/ La force F1 ne demande pas d'énergie car il n'y a pas de mouvement du point P1
2/ Le disque subit un couple comme si w1=0 et w2=0 car P1 est immobile, dans ce cas le travail est faible comparé à Fdtw1
3/ Le bras dans ce cas ne fournit pas de travail non plus (Fdtw1), comment l'expliquer ?

Enfin, c'est juste une hypothèse.

a+

[A voir en vidéo sur Futura]

[Dynamix]

3/ Le bras dans ce cas ne fournit pas de travail non plus (Fdtw1), comment l'expliquer ?

Les vitesse angulaire sont constantes , La somme des moments est nulle .
Il n' y a pas de translation
Le travail est nul
La force F1 n' existe pas .

[CZ48]

Le travail est sans doute nul mais la force F1 existe puisque c'est l'extérieur qui la fournit. Vous dites que les vitesses angulaires sont constantes, comment est ce possible puisque la force F1 va s'appliquer au point P1 pendant une durée dt, pourquoi w2 ne pourrait pas évoluer ? Si j'applique la force F1 à ce disque avec w2=0 et w1=0, il va se mettre à tourner, le bras aussi. Si F1 est présente en P1 pourquoi F2 ne serait pas présente ? Et si F2 est présente alors le bras travaille à Fdtw1.

Pourquoi parlez vous de translation ?

[Dynamix]

Si la force F1 ne produit pas de travail , l' énergie du système reste inchangée .
Mais c' est la cause de l' hypothèse fausse : le point P1 ne bouge .
Si F1 produit un travail , ω₂ n' est plus égal à ω₁ et donc le point ne déplace vers la gauche .

[CZ48]

J'ai indiqué que le point P1 ne bouge pas mais c'est lorsqu'il n'y a pas de force F1. Dès que F1 est appliquée le point P1 va bouger, donc effectivement la force F1 va nécessiter de l'énergie et le disque va ralentir. D'un autre côté le bras va fournir une énergie. Si je compare ces énergies :

1/ Le point P1 bouge très peu car c'est comme si on accélère un disque avec w2=0, donc le travail de la force est faible
2/ Le point P1 bouge très peu donc le disque perd peu d'énergie
3/ Le bras , lui, bouge beaucoup il tourne à w1, l'énergie est de Fdtw1, il n'y a qu'à regarder la distance d1 parcourue sur l'image précédente

C'est du qualitatif et non du quantitatif, je vais essayer de calculer, la somme devrait bien entendu être à zéro. Mais le raisonnement est il correct ?

Pour rappel, et sauf erreur de ma part, pour avec une vitesse nulle au point P1, il faut w2′=w1(d+r)/r, w2'=w2-w1 donc w2=w1(d+2r)/r

[Dynamix]

la force F1 va nécessiter de l'énergie

Une force ne "nécessite" pas de l' énergie , ça ne veux rien dire .
Ton erreur est dans le titre grosse comme un éléphant :
Travail d'une force stationnaire

[CZ48]

Re,

Au départ, effectivement je pensais que F1 ne travaillait pas c'est pourquoi j'ai mis ce titre mais impossible de changer maintenant...j'ai fait une erreur, c'est pas grave, si ?

Je n'utilise pas les bons termes, j'ai voulu dire "appliquer la force F1 pendant une durée dt et qui va se déplacer sur un dx va nécessiter de l'énergie" mais parfois les phrases deviennent longues.

Je n'ai même pas besoin de faire de calcul car le point P1 va bouger selon l'inertie du disque qui peut être plus ou moins importante par contre le travail du bras est toujours le même. Donc le raisonnement est faux et j'aimerai comprendre pourquoi.

A+

[Dynamix]

appliquer la force F1 pendant une durée dt et qui va se déplacer sur un dx va nécessiter de l'énergie

C' est tout le contraire .
La force F1 produit un travail F1.dx qui s' ajoute à l' énergie du système , mais ne demande pas forcément d' énergie .
Exemple si la force est produite par une butée fixe .

Je n'utilise pas les bons termes

Ce qui se conçoit mal s' énonce obscurément ,
et les mots pour le dire nous viennent difficilement

[CZ48]

A bien y regarder, si je fixe w2′=w1(d+r)/r alors le point avance quand même très, très peu dans le sens de w1, car les courbures des cercles sont différentes, ce que parcourt le point P1 sur la courbure du disque (en radial) il ne le fait pas selon la direction de la force. Si, P1 avance vers w1, il me suffit effectivement de le bloquer, donc la "force F1" peut se résumer à une butée et ne demande aucune énergie (c'est bien une force stationnaire). Par contre, comme le point bouge dans le sens de w1, la force F1 est donc de l'autre côté, le disque est accéléré et le bras décéléré. Mais j'ai le même problème, le bras perd une énergie de -Fdtw1 et le disque n'en gagne quasiment pas si son inertie est très grande. Qu'est ce qui ne va pas dans mon raisonnement ?

[CZ48]

Re,

Avec la force dans le bon sens selon les vitesses précédemment définies (j'ai changé l'orientation car l'image est très large):

stu.png

Et le détail des déplacements:

sxp.png

La force F1 va travailler sur la distance d1'(t)-d2'(t) sur le disque et la force F2 va travailler sur la distance d1b(t) sur l'axe. Donc la différence de travail est de F(-d1'(t)+d2'(t)-d1b(t)). D'où peut provenir mon erreur ?

A+

[CZ48]

Re,

Je viens de comprendre, c'est parce qu'il y a la réaction de l'arbre sur le disque: F3. Donc les travaux de F2 et F3 s'annulent, c'est bien cela ?



Reste à comprendre pourquoi avec la butée le disque augmente sa vitesse w2 et donc son énergie cinétique, car w1 reste constant. La force F1 travaille de F(-d2'(t)+d1'(t)), c'est pas énorme. Si vous avez une piste ?

A+

[CZ48]

Je viens de comprendre, je ne peux pas changer le couple sur le disque ou sur l'arbre. La force F2 applique un couple sur le bras et donc fournit un travail de -Fdtw1. La force F1 avec F3 applique un couple sur le disque et donc fournit un travail de Frtw2=Fdtw1 car w2=d/r*w1. Donc tout est bien dans le meilleur des mondes, la somme vaut zéro. Sauf que, le disque n'a pas la même inertie que l'ensemble {bras+disque}, c'est d'ailleurs impossible. Donc les vitesses de rotation w1 et w2 ne vont pas évoluer de la même manière. C'est la formule de Newton couple = inertie *accélération. Je peux prendre des inerties comme je veux pour le disque et le {bras+disque} ce sont des paramètres vraiment indépendants. Donc, si les vitesses n'évoluent pas de la même manière comment je peux avoir l'énergie perdue par l'arbre égale à l'énergie gagnée par le disque, ceci à chaque instant ?

J'aimerai bien un peu d'aide s'il vous plaît.

a+