Basculement d'un corps soumis à un choc d'un projectile

[Nicolas83]

Bonjour à tous,

Je sollicite votre aide aujourd'hui pour définir la méthodologie d’approche d'un problème plutôt commun mais que je ne sais pas par quel bout prendre : La stabilité au basculement d'un corps de masse m_s, de géométrie connue (parallélépipédique) posé sur le sol, et impacté par un engin de masse m_c arrivant à la vitesse v_c.

L'objectif est de définir la vitesse maximale d'impact faisant basculer le corps : v_cmax, sans glisser :

schéma2.png

Analyse du non glissement :

La condition de glissement pourrait être vérifiée une fois l'effort d'impact connu, ce qui ne me semble pas chose aisée du fait que l'énergie cinétique initiale se décompose en :

• Une énergie cinétique de translation du projectile
• Une énergie cinétique de translation du corps impacté
• Une énergie de rotation du corps impacté
• Une énergie de déformation élastique du corps impacté (dépendant de l'effort de choc et des rigidités du corps)

Bref, 1^er point à problème ...


Analyse du choc :

Concernant le basculement, j'ai essayer de réfléchir en m'aidant beaucoup de ce qui est écrit dans ce post : http://forums.futura-sciences.com/ph...e-bascule.html, en particulier les échanges entre matg22 et LFPR, que je saluent.
J'ai l'impression que je suis dans la même situation à la différence près que puisque le corps ne glisse pas (hypothèse que l'on devrait vérifier ensuite), alors un des coins inférieur est bloqué (très similaire à l'exercice 3 du §9.5 du fascicule de mécanique écrit par LFPR, vraiment très pédagogique).

Si je suis le même raisonnement, les paramètres après le choc v_c2, v_s2 et sont déduits de la vitesse d'impact du projectile avant le choc v_c1 et de la conservation des quantités de mouvement (linéaire et angulaire) ainsi que de l'énergie cinétique. Or, dans mon cas, le solide ne peut pas translater, il existe donc un effort horizontal extérieur (F_choc) "absorbant" une partie de la quantité de mouvement de l'ensemble; cette dernière n'étant donc pas conservée.

J'ai lu la remarque de LFPR, sur ce point qui indique dans le post précédent :

Le moment angulaire et le moment linéaire sont deux grandeurs physiques qui se conservent chacune de leur coté indépendamment l’une de l’autre.
Dans le cas de l’exercice 9, la poutre est libre de bouger et de tourner. Les deux quantités se conservent. Si la poutre est empêchée de se déplacer (à cause d’un axe ou des frottements avec le sol, alors le moment angulaire par rapport à l’axe de rotation sera conservé. Ainsi que le moment linéaire de l’ensemble : le projectile plus la poutre plus le support (la Terre, par exemple).

Mais il me semble qu'en considérant l'ensemble {corps, projectile, terre), la conservation de la quantité de mouvement (grandeur finie) impliquera une vitesse après impact négligeable compte tenu de la masse de l'ensemble (physiquement on sent que c'est pas ce choc qui va faire bouger la terre ...).

Une autre approche pourrait être d'écrire la "conservation" de la quantité de mouvement sous la forme :
m_c.v_c1 = m_c.v_c2 + m_s.v_s2 + E avec :



Le hic étant que je ne connais par le temps pendant lequel s'effectue le choc, ni même l'effort (en supposant qu'il soit constant durant dt ce qui n'est probablement pas le cas)... Du coup je suis un peu coincé !

Déjà y a t il selon vous des énormités dans mon raisonnement sur cette partie ? Avez vous des idées sur la façon de déterminer les paramètres juste après impact ?


Analyse de non basculement :

En imaginant les paramètres après choc connus (v_c2, v_s2 et ), je pensais :

SOIT :
1. appliquer le théorème du moment dynamique autour de l'axe pour déterminer l'équation du mouvement

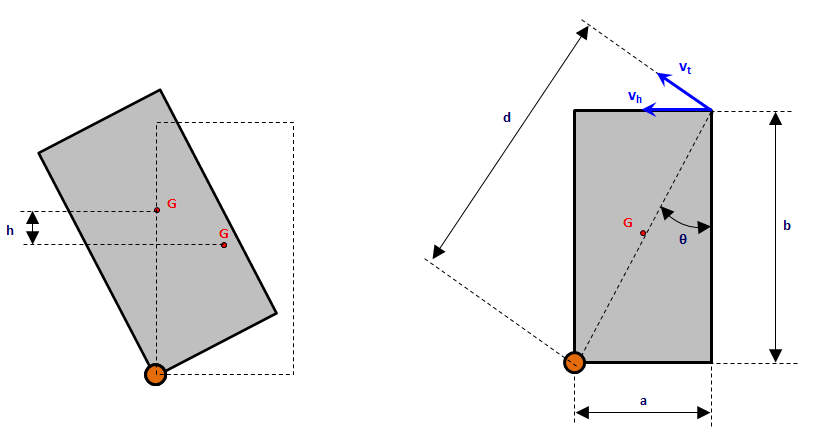
schéma.png

2. relier l'angle maximal de rotation à la vitesse angulaire et donc à la vitesse initiale du projectile vp


SOIT :

1. directement écrire que la variation d'énergie cinétique du corps est égal au travail des forces appliquées, en l’occurrence le poids, et donc que :

• h étant la hauteur effective amenant le CdG dans le plan vertical passant par l'axe fixe
• la vitesse angulaire initiale du corps après le choc

Qu'en pensez vous ?

Je vous remercie par avance pour votre aide et n'hésitez surtout pas si quelque chose n'est pas clair

Cordialement
-----

[LPFR]

Bonjour et bienvenu au forum.
Je suis content que mon fascicule vous ait plu. Et merci de le dire.

Je crois que vous avez bien compris le problème.

Suivant le type de choc, une partie de l’énergie peut être transformée en chaleur quand le choc n’est pas élastique.
Si le projectile est absorbé par le corps, l’énergie n’est pas conservée. On peut aussi étudier le cas où le projectile rebondit. Mais c’est un peu plus compliqué.

Donc, ici il faut se rabattre sur ce qui se conserve : le moment angulaire (=cinétique) et le moment linéaire.
Dans votre cas, comme le bas ne peut pas glisser, le moment linéaire projectile+corps, ne se conserve pas.
Il ne nous reste que el moment angulaire.

Donc, calculez le moment angulaire avant le choc par rapport au coin qui servira de pivot, (avant le choc, il n’y a que le moment angulaire du projectile).
Après le choc le moment angulaire sera celui de l’objet tournant autour du pivot. Il fut donc utiliser le moment d’inertie autour de cet axe et non celui autour de l'axe qui passe par le centre de masses.
Au revoir.

[Nicolas83]

Bonjour et merci pour votre réponse.

Si je comprend bien ce que vous dites :

Donc, calculez le moment angulaire avant le choc par rapport au coin qui servira de pivot, (avant le choc, il n’y a que le moment angulaire du projectile).
Après le choc le moment angulaire sera celui de l’objet tournant autour du pivot.

je le traduirai par :




Pourtant j'aurais intuitivement écrit :



En l'occurrence le projectile a une masse bien plus élevée que le support ce qui tendrait à confirmer le fait qu'il ne rebondit pas... Donc finalement, écrire ce que vous me proposez revient à dire que le projectile s'encastre dans le support, les 2 corps possèdent alors la même vitesse au centre des masses, mais comme de toute façon le support ne peut se déplacer horizontalement, alors cette vitesse est nulle; d'où votre formulation. Ais je bien saisi ?

Si oui, l'hypothèse de blocage du support est primordiale... Or cette "fonction" est assuré par le non glissement de l'ensemble ce qui du coup risque de ne pas être le cas.


Résolution dans le cas d'un blocage réel :

La conservation de la quantité de moment permet de déterminer la vitesse angulaire initiale de l'objet et donc l'énergie cinétique de rotation disponible. En limitant cette énergie à l'énergie potentielle de pesanteur entrainant une élévation du centre des masses du corps le plaçant au droit de l'axe de rotation, on peut déterminer la vitesse initiale limite du projectile n’entraînant pas le basculement.

Conservation de la quantité de moment :


Transformation de l'énergie cinétique de rotation du corps en énergie potentielle :



Soit :


Et donc en posant H, la hauteur entre le point d'impact et l'axe de rotation :



L'approche vous semble t elle cohérente ?


Justification du blocage réel :

Sur ce point je n'ai pas d'idée puisque pas d'information sur le choc lui même.


Petite question complémentaire :

vous dites :

Si le projectile est absorbé par le corps, l’énergie n’est pas conservée. On peut aussi étudier le cas où le projectile rebondit.

1. J'ai du mal à saisir où est l'énergie complémentaire ?
2. Je pensais que l'effet de "rebond" n'était pas un hypothèse à poser mais bien une conséquence des masses en présence et du coefficient de restitution ? En supposant ce coefficient à 1, l'énergie devrait se conserver ?
3. Comment feriez vous pour étudier le cas où cela rebondit ?

Merci d'avance pour votre temps

Cordialement

[LPFR]

Re.

C’est correct. Et c’est ce qu’il faut utiliser si le projectile traverse l’objet.
Le problème est qu’il faut connaître la vitesse de sortie.

me proposez revient à dire que le projectile s'encastre dans le support, les 2 corps possèdent alors la même vitesse au centre des masses, mais comme de toute façon le support ne peut se déplacer horizontalement, alors cette vitesse est nulle; d'où votre formulation. Ais je bien saisi ?

Pas tout à fait. Si le projectile s’encastre, alors le moment d’inertie est celui de l’objet plus celui du projectile. Et aucun des deux n’a de vitesse nulle : l’ensemble tourne autour de l’axe.

La conservation de la quantité de moment permet de déterminer la vitesse angulaire initiale de l'objet et donc l'énergie cinétique de rotation disponible. En limitant cette énergie à l'énergie potentielle de pesanteur entrainant une élévation du centre des masses du corps le plaçant au droit de l'axe de rotation, on peut déterminer la vitesse initiale limite du projectile n’entraînant pas le basculement.

Conservation de la quantité de moment :

Je ne sais pas ce que vous appelez « quantité de moment ». Est-ce le moment angulaire (=cinétique) ?
On dirait, à cause de la formule qui suit.
Mais je vous suggère de garder les dénominations standard.

L'approche vous semble t elle cohérente ?

Oui. Sauf que je ne sais pas quel cas vous étudiez : blocage du projectile ?
Si c’est le cas Ja est le moment d’inertie du corps plus le projectile.
Le ‘h’ est la hauteur du centre de masse (de l’ensemble) quand celui-ci est à la verticale du pivot.

Justification du blocage réel :

Je n’ai pas réfléchit à ce cas. Il faut voir ce qui se passe pendant l’impact, entre le couple qui à tendance à faire tourner l’objet, el la force (en le couple) exercée par le support sur le pivot. Ceci doit permettre de calculer le coefficient de friction pour qu’il n’y ait pas de glissement. Mais ce n’est pas encore assez clair dans ma tête.

J'ai du mal à saisir où est l'énergie complémentaire ?

Après un choc plastique, l’énergie totale est plus faible que l’originale. La différence s’est transformée en chaleur.
Dans un choc élastique, (coefficient de restitution = 1), toute l’énergie se conserve. Dans la réalité, aucun choc n’est complètement élastique. Il y a toujours une partie d’énergie perdue. Par contre on peut faire des chocs totalement plastiques.

Je pensais que l'effet de "rebond" n'était pas un hypothèse à poser mais bien une conséquence des masses en présence et du coefficient de restitution ? En supposant ce coefficient à 1, l'énergie devrait se conserver ?

Le rebond ou le chocs plastique est bien une conséquence de la nature des objets, qui détermine le coefficient de restitution. Mais c’est une hypothèse dans l’énoncé du problème.

Comment feriez vous pour étudier le cas où cela rebondit ?

Je pense que je « tricherais un peu », en donnant du jeu à l’axe du pivot en en étudiant la collision comme si l’objet était libre dans l’espace. Evidement, cette triche n’est valide que si la collision est suffisamment rapide.
A+

[A voir en vidéo sur Futura]

[Dynamix]

Salut
Avec un coef de restitution de 1 ça rebondit .

Petit résumer des differents cas :
Cr = 1 => choc parfait sans perte d' énergie avec rebond
Cr entre 1 et 0 => choc plus ou moins mou avec perte d' énergie et rebond
Cr = 0 =>choc totalement mou : La balle s' encastre dans l' obstacle . Après choc la balle et l' obstacle ont la même vitesse
Cr entre 0 et -1 => la balle traverse l' obstacle avec perte d' énergie
Cr = -1 => pas de choc

[Nicolas83]

Re,

Le problème est qu’il faut connaître la vitesse de sortie.

En effet c'est bien le problème et j'ai l'impression qu'en faisant l'hypothèse d'une structure bloquée au sol, je n'ai plus assez d'équations de conservation pour définir cette vitesse, que je dois finalement imposée (hypothèse d'absorption ou de rebond).

Si le projectile s’encastre, alors le moment d’inertie est celui de l’objet plus celui du projectile.

Vous faites bien de le préciser, j'étais passer à travers ... En l'occurrence, ma structure est un cadre de tube creux de base carrée (700 mm) sur une hauteur de 6m (masse à vide une centaine de kilo, masse en charge 1500kg). Le "projectile" lui est un chariot de manutention relativement volumineux de masse 5 tonnes environ... C'est un David contre Goliath.
Le hic si l'on considère le Ja de l'ensemble c'est qu'il va bien falloir une liaison mécanique suffisamment solide pour soulever le chariot. or ce n'est probablement pas le cas puisque seul le contact du au choc existe. Cela remet probablement en question toute l'approche...

Je ne sais pas ce que vous appelez « quantité de moment ». Est-ce le moment angulaire (=cinétique) ?
On dirait, à cause de la formule qui suit.
Mais je vous suggère de garder les dénominations standard.

C'est tout à fait cela, abus de langage de ma part.

Oui. Sauf que je ne sais pas quel cas vous étudiez : blocage du projectile ?
Si c’est le cas Ja est le moment d’inertie du corps plus le projectile.
Le ‘h’ est la hauteur du centre de masse (de l’ensemble) quand celui-ci est à la verticale du pivot.

Oui c'est bien le cas de blocage du projectile que j'ai envisagé dans la démarche analytique précédente. Mais clairement "Ja" de l'ensemble sera une inconnue impossible à déterminer...
La hauteur "h" par contre est l'élévation du CdG de la structure entre sa position "posée au sol" et la position "limite de basculement"
schéma3.png

Je pense que je « tricherais un peu », en donnant du jeu à l’axe du pivot en en étudiant la collision comme si l’objet était libre dans l’espace. Evidement, cette triche n’est valide que si la collision est suffisamment rapide.

Effectivement ça pourrait être une solution, d'autant plus que le "pivot" n'est pas matériel, c'est simplement la résistance par frottement de la structure sur le sol.

@ Dynamix : Merci pour ces précisions sur le coefficient de restitution...


Bilan :

Au final la problématique n'est pas simple et l'hypothèse, majeure, de blocage en translation est loin d'être acquis compte tenu des grandeurs physiques en jeu

• Soit, le frottement est suffisant et dans ce cas la quantité de mouvement ne se conservant pas, il faut faire l'hypothèse d'une absorption du projectile par la structure PUIS une évaluation correcte du Ja de l'ensemble. Mais honnêtement je vois mal le chariot basculer avec la structure ...
• Soit la structure glisse ET bascule, et le problème se traite classiquement avec une structure non bloquée et donc conservation des quantités de mouvement et de l'énergie cinétique (hypothèse d'un choc élastique me parait raisonnable).

Dernières possibilités d'analyse du problème :

1. Approche Extrêmement simplifiée:

Transformation de toute l'énergie cinétique de translation du chariot en énergie cinétique de rotation de la structure. Le résultat de la vitesse max serait alors :
.

Personnellement le fait que ce résultat ne dépende pas de la hauteur à laquelle l'impact à lieu me gêne ...


2. Approche basée sur votre astuce de découplage :

Le raisonnement se mène en 2 étapes :

1. Analyse d'une collision entre un projectile (le chariot) et la structure "libre" de faire ce qu'elle veut
2. Analyse dynamique de la structure posée au sol et bloquée en translation en son coin, et soumis à des vitesses initiales et précédemment calculées dans l'analyse du choc

schéma4.png

Pour la première partie, application des 3 lois de conservation et détermination des vitesses linéaires de la structure et du chariot, ainsi que de la vitesse angulaire de la structure (découplée du chariot cette fois).
Pour la seconde, application du théorème du moment dynamique sur l'axe fixe (coin intérieur) sur une structure bloquée horizontalement sur un ressort de raideur équivalente à celle de la structure pour un chargement m. du CdG.

• Transformation de l'énergie cinétique de translation en énergie potentielle élastique : la force d'appui vaut alors :
• Vérification du non glissement par :
• Vérification de la stabilité en reliant et à l'angle maximal autorisé : équation de mouvement de la structure

Bon cette équation différentielle est équivalente à celle d'un pendule pesant avec un terme supplémentaire donc facilement solvable pour de petits angles, ce qui n'est PAS le cas ici => Résolution numérique.

L'approche est un peu différente et plus complexe à mettre en oeuvre mais me semble plus proche de la réalité. Qu'en pensez vous ?

Bien cordialement

PS : je suis désolé pour les pavés à chaque fois mais je vois pas comment expliquer plus simplement ...

[LPFR]

Re.
Je viens de lire en diagonale votre message.
Je pense qu’avant d’aller plus loin, il vaudrait mieux que vous nous expliquiez le problème réel avec ses dimensions, ses vitesses et ses masses.
Car il n’est pas évident que l’approximation du projectile qui s’incruste soit vraiment la bonne.

Pour ce qui concerne le projectile qui traverse, il est évident que ça dépend de l’âge du capitaine… et de son embonpoint. Vous ne pouvez pas savoir (sauf cas particuliers) si un projectile traversera une cible.
Au revoir.

[Nicolas83]

Re et merci de m'accorder de votre temps ...

Effectivement quelques détails supplémentaires permettraient certainement de mieux appréhender la problématique d'ensemble.

1. La structure :

Il s'agit de l'empilement de 3 cadres tel que celui sur la photo ci dessous :
CadreSeul.png

Le premier cadre est posé au sol et les 2 suivants sont justes empilés les uns sur les autres. On pourra considérer en première approche que l'ensemble forme une structure sans liaisons cinématiques. L'ensemble donne :
Structure.png

Caractéristiques :
Dimensions de la base : 1125 x 1125 mm
Hauteur d'un cadre : 2154 mm
Hauteur totale : 6462 mm
Masse de la structure vide : 300 kg
Masse de la structure en charge : 1800 kg
Moment d'inertie au CdG : Inconnu pour le moment

=> Je ferais le calcul en négligeant les contributions élémentaires de chaque barre :


Avec :
m : Masse d'un cadre (100kg)
d_i : distance d'un centre de cadre à l'axe fixe


2. Le "projectile :

Le "projectile" est un chariot de manutention de 5 tonnes du type de celui sur les photos ci dessous :
projectile.png


3. Problématique :

Il est possible, pendant les phases d'exploitation, qu'un chariot heurte la structure. L'objectif de l'étude est de déterminer la vitesse maximale avec laquelle il peut la heurter sans la faire tomber / Basculer dans 2 cas :

• Structure pleine
• Structure vide

Il parait raisonnable de pensée que plus le choc a lieu haut sur la structure, plus le risque de basculement est important et que la stabilité est d'autant moins acquise que la masse de la structure est basse. Le cas de la structure à vide semble donc le plus pénalisant.

De plus, étant donné les masses mises en jeu ainsi que l'élancement de la structure, on s'attend à des vitesses extrêmement basse lorsque la structure est pleine; quasi négligeable lorsque la structure est vide. Il est donc possible que la conclusion soit que la stabilité ne peut être garantie en cas de contact avec le chariot quelque soit la vitesse.

De plus en pratique, un choc intervient si l'opérateur "oublie" son environnement. Dans ce cadre, le chariot aura aussi probablement une énergie motrice qui serait susceptible de continuer à s'exercer une fois le contact établi. La collision ne serait plus "libre" mais plutot "forcée". Cette hypothèse est exclue des analyses, considérant que cette situation conduit irrémédiablement à la chute de la structure.


Ces données vous permettent elle de voir la problématique dans son ensemble ?

Cordialement

[LPFR]

Bonjour.
Je viens le lire la description du problème réel.
Je pense que le modèle projectile + poutre n’est pas adapté.
Je vais réfléchir et je vous répondrai plus tard (c’est après-midi, probablement).
Au revoir.

[Nicolas83]

Bonjour,

Je vais essayer de mettre des valeurs numériques sur l'approche que je vous ai présentée hier, peut être que les résultats mettront directement la méthodologie en défaut.

Je pense que le modèle projectile + poutre n’est pas adapté.
Je vais réfléchir et je vous répondrai plus tard (c’est après-midi, probablement).

Je suis bien sur très preneur de l'issue de votre réflexion sur ce point.

Merci encore pour votre aide et votre regard sur cette problématique.

Bien cordialement

[LPFR]

Bonjour.
Comme je vous disais le modèle projectile plus poutre n‘est pas adapté.
Vous avez un chariot avec une masse énorme comparée aux étagères.
Faire un calcul précis en tenant compte que le choc ne se fera pas avec le bas du chariot mais avec la partie « élévateur », nécessairement plus légère, risque d’être compliqué.
Je pense qu’il faut être pessimiste et supposer que le haut a la masse du chariot. On saura que la réalité ne peut pas être pire que cette simplification.
Si le choc est plastique, on peut supposer que l’endroit de l’étagère prend la vitesse du chariot. Si le choc est élastique, alors l’étagère prend le double de la vitesse du chariot. On se retrouve dans un cas similaire à un gros club de golf qui tape une balle beaucoup plus légère. (L’avantage est que dans le golf on connaît le coefficient de restitution, pas ici).
Si les fourches tapent sur une boite stockée, la suite dépend de ce qui a dans la boite en en quoi elle est faite.
On peut prendre le cas le plus pessimiste qui est que le chariot tape sur un des montants des étagères.

Avec mes suppositions (pessimistes) on arrive à simplifier le problème à celui d’étudier ce qui arrive quand un point d’une étagère part avec une vitesse horizontale connue.

Il faut, évidement étudier les conséquences suivant le point d’impact. Cela fait un tas de cas différents
Est ce que les étagères sont fixées à leurs voisines latérales ?
Si c’est le cas, le montage est bien plus stable, et l’étude vraiment compliqué. Car on tombe plutôt sur la RDM (résistance de matériaux) et là, je ne connais pas grand-chose (mais d’autres foristes dominent le sujet).

Le cas le plus simple est celui de la dernière étagère non reliée à ses voisines et cognée en haut. À partir de la vitesse du point d’impact, on calcule la vitesse angulaire, puis, avec le moment d’inertie, l’énergie de l’objet. Et on peut voir si le centre de gravité dépasse la zone d’équilibre (le rectangle de sustentation).
Le cas suivant est la dernière étagère cognée en bas. Ça se complique. Elle peut glisser sur la seconde, ou l’entraîner avec elle (ou les deux). Pivoter sur la seconde en entraînant celle-ci à pivoter sur la première.

Je crois que c’est tout pour la dernière. Mais il reste encore la seconde et la base (peut-être pas si la base est fixée au sol).
On continuera la réflexion quand vous aurez digéré mon baratin.
Au revoir.

[Jaunin]

Bonjour LPFR,
J'avais répondu à un même genre de discussion sur le "carambolage" d'un Clarke avec une étagère ou une plateforme.
Je viens de faire une recherche, mais je n'ai rien trouvé, je ne me souviens plus du titre.
J'ai peut être encore un fichier ?
Cordialement.
Jaunin__

[LPFR]

Bonjour Jaunin.
Vous tombez bien. Surtout pour Nicolas83.
Car comme je lui ai dit, il est possible que l’on soit plutôt dans la RDM et il aura de la chance si vous l’aidez.
Au revoir.

[Nicolas83]

Bonjour à vous Jaunin, cela faisait longtemps ....

Si je comprend bien votre analyse :

Si le choc est plastique, on peut supposer que l’endroit de l’étagère prend la vitesse du chariot. Si le choc est élastique, alors l’étagère prend le double de la vitesse du chariot. [...]
Avec mes suppositions (pessimistes) on arrive à simplifier le problème à celui d’étudier ce qui arrive quand un point d’une étagère part avec une vitesse horizontale connue.

et

Le cas le plus simple est celui de la dernière étagère non reliée à ses voisines et cognée en haut. À partir de la vitesse du point d’impact, on calcule la vitesse angulaire, puis, avec le moment d’inertie, l’énergie de l’objet.

Alors la vitesse horizontale de la structure est connue et vaut celle du chariot ou le double selon que le choc est complètement plastique ou élastique (intervention de la RDM dans ce pb)


Connaissant la vitesse horizontale v_h, on déduit la composante tangentielle par :






Schéma.png


Puis la vitesse angulaire :



Connaissant J_a autour de l'axe de rotation (coin inférieur) et en appliquant la conversion d'énergie cinétique de rotation en énergie potentielle de pesanteur :





D'où connaissant la hauteur limite "h_l" correspondant à la position ou le CdG est aligné avec l'axe de rotation :



Interprétation :

Au vue de la formule, j'ai du mal à interpréter physiquement que :

• La vitesse maximale autorisée augmente avec la distance "d" et donc la hauteur d'impact : Intuitivement, j'aurais dit l'inverse...
• La vitesse maximale autorisée diminue quand le moment d'inertie augmente : là encore plus J est élevé, plus il faut d'énergie pour mettre le système en rotation, j'aurais donc intuité le contraire...
• Le résultat ne dépend plus directement de la masse du chariot (même si c'est bien le rapport des masses et des rigidités qui ont permis de déterminer vh) : l'énergie cinétique initiale du système en dépend quand même largement pourtant...

Ce sont des réactions à chaud donc j'espère ne pas dire trop d'âneries.


Analyse en adoptant la conservation du moment cinétique :

Conservation du moment cinétique :



Conversion de l'énergie cinétique de rotation de la structure en énergie potentielle de pesanteur :





Et donc la vitesse maximale autorisée :



Interprétation :

Dans ce cas là, la vitesse maximale autorisée semble :

• Diminuer d'autant que la masse du chariot et la hauteur d'impact augmente
• Augmenter d'autant que le moment d'inertie augmente

Cela ne permet pas de déterminer l'effort d'impact et donc la condition de non glissement mais cela semble assez physique, qu'en pensez vous ?

Cordialement,

[Nicolas83]

Sur ma lancée, je pensais à l'approche suivante :

En considérant le choc élastique (pas de perte de chaleur ni de plastification des structures, plutôt souples), le théorème de l'énergie cinétique permet de dire que cette dernière se conserve puisque la somme des travaux des forces est nulle (pas de force travaillante si le chariot et la structure ne se touche pas après le contact)

En ajoutant à cela la conservation du moment cinétique (comme ma version précédente), on obtiendrait :





Le système donne 2 équations à 2 inconnues qui se résout facilement par substitution :



En reportant dans la première :





En écartant la solution où la vitesse angulaire est nulle :



Finalement :



Interprétation :

2 points me semblent intéressants à souligner :

• Le cas ou la masse du chariot est très grande devant le moment d'inertie de la structure
• Le cas ou le moment d'inertie équivalent du chariot est identique à celui de la structure

En effet dans la première situation, lorsque la masse du chariot est très élevée ou que la hauteur d'impact est très grande alors :




Sous cette forme, cela correspond exactement à celle du post précédent obtenue en considérant l'approche que vous proposez et un choc parfaitement élastique, à savoir que la vitesse horizontale de la structure serait le double de celle du chariot...


Dans la 2ème situation, l'étude de l'énergie cinétique de rotation de la structure donne :





En utilisant l'hypothèse de cette situation :





=> Toute l'énergie cinétique du chariot est transformée en énergie cinétique de rotation de la structure, un peu comme dans une collision de 2 billes de même masse où la première s'arrete et l'autre repars à la vitesse initiale :


Compte tenu de ces résultats semblants cohérents, Pensez vous que cette approche généralise celle que vous aviez tout à l'heure quelque soit la masse du chariot ?

Bien Cordialement,

PS: Il se fait tard donc j'espère ne pas avoir écrit d'âneries... Si c'est le cas, n'hésitez pas

[LPFR]

Bonjour.

Alors la vitesse horizontale de la structure est connue et vaut celle du chariot ou le double selon que le choc est complètement plastique ou élastique (intervention de la RDM dans ce pb)

Ce n’est pas la vitesse horizontale de la structure. Mais celle du point d’impact. C'est-à-dire que ce que l’on a est la vitesse tangentielle du point d’impact.

Pour vos conclusions :
Dans la mesure où on suppose que la vitesse acquise par un point de la structure est celle du chariot (ou le double), oui, les collisions plus hautes sont moins méchantes que les basses.
Comme le moment d’inertie est proportionnel à la masse, ce qui compte est le coefficient qui multiplie la masse dans le moment d’inertie. Si la masse est surtout en haut de la structure, la vitesse pour la faire basculer est plus faible que si la masse est en bas de la structure.
Dans la mesure où on considère que la masse du chariot est « infinie », effectivement, le résultat ne dépend que de sa vitesse.
Après le choc, le moment cinétique ne se conserve pas. Il y a le couple dû au poids qui diminue le moment cinétique.
Ce qui se conserve est l’énergie.
Au revoir.

[Nicolas83]

Bonjour,

Ce n’est pas la vitesse horizontale de la structure. Mais celle du point d’impact. C'est-à-dire que ce que l’on a est la vitesse tangentielle du point d’impact.

Je comprend cette remarque et suis en phase avec cela.

Dans la mesure où on suppose que la vitesse acquise par un point de la structure est celle du chariot (ou le double), oui, les collisions plus hautes sont moins méchantes que les basses.
Comme le moment d’inertie est proportionnel à la masse, ce qui compte est le coefficient qui multiplie la masse dans le moment d’inertie. Si la masse est surtout en haut de la structure, la vitesse pour la faire basculer est plus faible que si la masse est en bas de la structure.

Effectivement vous avez raison, physiquement je le comprend mieux dit comme cela.
Nota : Ces observations semblent cohérentes de la dernière formulation de vitesse limite déterminée dans le cas de la 3eme analyse (2e post et rappelée ci dessous).

Après le choc, le moment cinétique ne se conserve pas. Il y a le couple dû au poids qui diminue le moment cinétique.
Ce qui se conserve est l’énergie.

Je suis d'accord avec cela, et il me semble que c'est la traduction de cette loi qui conduirait à l'équation différentielle qui régit le mouvement.
J'ai effectivement reposée la 2e analyse sur ce principe et comprend donc les conclusions erronées qui vont de paire avec votre commentaire au dessus.

Cependant L'analyse dans le second post me semblait être plus en adéquation avec ce que vous dites :

1. Conservation du moment cinétique et de l'Energie cinétique pendant la phase de choc uniquement => Lien entre vitesse angulaire de la structure, la vitesse linéaire du chariot et caractéristiques des 2 corps
2. Conservation de l'énergie cinétique uniquement pour vérifier la stabilité : Conversion Enegie cinétique de rotation => Energie potentielle de pesanteur

Elle conduit au résultat suivant




Cette conclusion vous semble t elle donc plus juste ?

Cordialement

[LPFR]

Re.
Je me suis en peu perdu dans vos variables.
Pour mc et ms, ça l’air évident : ‘c’ pour chariot et ‘s’ pour ??
Mais ‘b’ et je ne suis pas sur.
Je ne trouve pas la position de l’impact.
A+

[Nicolas83]

Re,

m_c et m_s correspondent respectivement à masse chariot et masse structure.

"b" correspondant justement à la hauteur du choc vis à vis de l'axe supposé fixe (coin inférieur gauche sur le schéma).
h_l est en fait précsier seulement "h" sur le schéma et correspond à l'élévation du centre de gravité de la structure entre sa position initiale (posée à terre) et sa position limite de stabilité (CdG dans le plan vertical passant par l'axe fixe)

Je vous remet le schéma en question ci dessous :


Est ce plus clair ?

[LPFR]

Re.
Oui. C’est plus clair.
Je n’avais pas saisi que le choc était tout en haut de la structure.
Mais ce qui est imposé est Vh.
Donc Vt = Vh/cos θ
Et la masse du chariot ne rentre pas en ligne de compte. Elle est déjà rentrée quand on a dit qu’elle imposait la vitesse Vh.
A+

[Nicolas83]

Re,

Je n’avais pas saisi que le choc était tout en haut de la structure.

Oui pour l'instant c'est le cas que j'imagine

Mais ce qui est imposé est Vh.
Donc Vt = Vh/cos θ

Exact. Et d'ailleurs c'est bien en posant cette équation que la formulation généralisée tend vers la formulation que vous proposez lorsque la masse du chariot est très grande par rapport à celle de la structure (vitesse de cette dernière imposée à celle du chariot ou au double).


Conclusion :
Pour la suite de l'étude et ne voyant pas d'arguments contraires, je pense retenir La formulation généralisée suivante pour la vitesse limite du chariot avant basculement de la structure :


Puisque :

• tendant vers des solutions physiquement explicables dans les cas limites,
• Respectant les principes de conservation d'énergie et de moment cinétique lors du choc
• Respectant le principe de conservation d'énergie après le choc

Les hypothèses retenues pour en arriver la sont :

1. Le choc est complètement élastique
2. Les énergies nécessaires pour déformer les corps (structure et chariot) sont négligées (en pratique elles ne le sont peut être pas)
3. L'effort de choc reste inférieur au seuil de glissement, ce qui permet de modéliser le pivot dans le coin inférieur

Remarque :
La résolution du problème permettant de définir aussi la vitesse après choc du chariot, Je pense que nous pourrions, connaissant le temps de choc, définir l'effort d'impact en le reliant à la variation de la quantité de mouvement... Ainsi la vérification de l'hypothèse de non glissement pourrait être réalisée :


Enfin, il me semble que l'on pourrait encore affiner le calcul en tenant compte de l'énergie de déformation élastique de la structure dans le bilan énergétique, en reliant cette dernière à l'effort de contact, connaissant la rigidité de la structure :






Et "k" étant déterminer par un calcul test ou analytiquement...

Au final, le système à résoudre serait de dimension 4 :

1. Bilan d'énergie : cinétique + déformation élastique
2. Conservation du moment cinétique
3. Relation liant les efforts extérieurs à la variation de quantité de mouvement (là il faut connaitre la durée du choc )
4. Relation liant la déformation élastique à l'effort la générant

Si vous voyez quoique ce soit qui remette en question cette approche, n'hésitez pas.

De mon côté je vais mettre des valeurs numériques sur ce problème et viendrait les postées.

Je vous remercie grandement pour votre aide et vos remarques pertinentes ! Sans vous, je ne me serais probablement perdu dans l'analyse...

Bien cordialement

[LPFR]

Re.
On peut effectivement tenir compte de la déformation et l’élasticité de la structure. Mais c’est un tout autre problème.
Jaunin peut peut-être vous donner des idées.
Ce n’est pas mon domaine.
A+