Oscillateurs couplés

[invite1d656ca6]

Bonjour,
j'ai un exercice dans lequel je suis coincé je vous met l'énoncé :

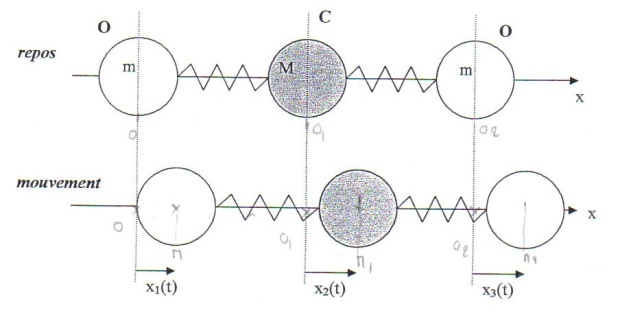
Dan la molécule de CO₂, on peut modéliser la double liaison C=0 par un ressort de raideur k et de longueur l₀. Les 3 atomes peuvent se déplacer le long d'un axe x. A un instant t, leurs postions, notées x₁, x₂, x₃ sont repérées par rappert a leurs positions au repose. (M : masse du carbone m masse de l'oxygène)

1) etablir les équtions différentielles

2) ON introduit les nouvelles fonctions u(t) = x₁(t) - x₂(t) et v(t) = x₃(t) - x₂(t)) mesurant l'écart entre les positions desDonner les équations différentielles portant sur les focntions u(t) et v(t). Pour simplifier, on introduit w₀²= k/M et r=1+M/m

alors moi j'ai aboutis a 3 equations différenielles sur les 3 masses ;
sur masse M :equation (1)
-kx₂ + k (x3-x2) = M d²x2/dt²

sur le premier bloc m : (2)
kx1=md²x1/dt²

sur le 2eme bloc m (3)
kx3=m d²x3/dt²

j'ai additioné (2) et (3) :
ku(t) = m (d²x1/dt² + md²x3/dt²)
euqation 1

-kx₂ + kv(t) = M d²x2/dt²

Voila je n'arrive pas a tou mettre ebn fonction de u et v comment dois je procéder ?
Pouver vous m'aider svp ?

Je vous remercie d'avance.
-----

[invite70e57eb7]

Je ne trouve pas les mêmes équations :

k.(x2-x1)=m d²x1/dt²
-k.(x2-x1)+k.x3=M d²x2/dt²
-k.(x3-x2)=m d²x2/dt²

ce qui fait après simplifications :
-W₀².u=r.d²x2/dt² + d²v/dt²

C'est pas franchement mieux...quelqu'un d'autre à une idée ??

[invitea3eb043e]

Je ne trouve pas les mêmes équations :

k.(x2-x1)=m d²x1/dt²
-k.(x2-x1)+k.x3=M d²x2/dt²
-k.(x3-x2)=m d²x2/dt²

ce qui fait après simplifications :
-W₀².u=r.d²x2/dt² + d²v/dt²

C'est pas franchement mieux...quelqu'un d'autre à une idée ??

Dans la seconde équation, c'est
-k(x2-x1) + k (x3-x2) = Md²x2/dt²

On introduit les fonctions u et v sans problème mais il ne faut pas oublier une relation supplémentaire :
mx1 + Mx2 + mx3 = 0
qui permet de s'affranchir du mouvement d'ensemble de la molécule (centre de gravité en translation uniforme : sans intérêt : prendre le référentiel du centre de masse qui est d'inertie).
Normalement sur les équa diff, ça doit apparaître quand on calcule la dérivée seconde de mx1 + Mx2 + mx3 en additionnant judicieusement.

[invite1d656ca6]

ba je comprends pas, les forces qui s'exercent sur le premier ressort c'est que la force de rappel ? et elel ne s'écrit pas comme ça : kx1 ?

[A voir en vidéo sur Futura]

[invite1d656ca6]

non c bon j'ai compris lol je retire ma kestion

[invite70e57eb7]

Dans la seconde équation, c'est
-k(x2-x1) + k (x3-x2) = Md²x2/dt²

Ah oui, c'est vrai ! Le reste ne présente pas vraiment de difficulté. On retombe bien sur une equa diff du second degré très facile à résoudre.

Merci pour la correction Jeanpaul !!

[invite4b31cbd7]

http://gilbert.50g.com/ondes/devoirs/D2_sol.pdf

Voir le problème 2.

En passant, le site du M.I.T offre des opencourse, et celui sur les ondes est particulièrement bien.

http://ocw.mit.edu/OcwWeb/Physics/8-...ures/index.htm

[invite1d656ca6]

J'ai encore quelques questions a vous poser voila j'ai un autre problème sur un exercice du meme genre.

D'abord il me demande les allongements des 2 ressorts a l'équilibre deltal1 et deltal2
moi j'ai trouvé que deltal1 = OO1 et deltal2 = OO2-OO1

Ensuite ils me posent :
Le bloc 1 est soumis a une force F=Focos(wt) u_x.
Déterminer en fonction de deltal1, deltal2, x1(t), x2(t) les lalongemetns notés delta^'1 et delta^'2.
Mais je dois me trompée quelque part puisque moi je trouve : l'allongemetn pour le bloc 1 c'est la distance OM1 - OO1= O1M1=x1
et pour le resssort 2 : allongement serait : M1M2 -O1O2= -x1+x2

Pouvez vous me dire mes erreurs svp ?
Merci d'avance !

[invite742846b3]

Tu suppose que l'allongement d'un ressort est sa longueur mais je pense que c'est juste son accroissement. A l'équilibre un ressort a comme longueur, sa longueur naturelle ou et son accroissement est nul. mais dans ce cas ci, on dirait que la gravitation joue un role, non ? vu que l'axe est vertical. doit-on en tenir compte ?
si oui, l'accroissement du premier ressort serait du poids (M1+M2)g divisé par k1 et lpour le second ressort gM2/k2. Voici pour la partie 'à l'équilibre'.

[invite1d656ca6]

a oui c vrai ! javé oublié le poids !
Mais hors équilibre est ce que je peux dire que pour le 1er ressort la force de rappel vaut Fr= -k(OM1-OO1)=-kO1M1=x1 donc delta^'= x1 ?

et pour le ressort 2 je ne peux pas faire Fr2= -k(M1M2 -O1O2) = =-k(-x1+x2) ?

[invite1d656ca6]

ah oui a léquilibre delta1= ( M1+M2)g/k1
delta2= M2g/k2

donc hors équilibre, pr le ressort 1 Fr+P= -k1x1 +(M1+M2)g = -k1x1 +k1delta1= -k1 ( x1 -delta1)
donc deltaprime1= x1 - delta 1

pour le ressort 2 Fr2 +P2 = -k2(x2-x1) + M2g = -k2(x2-x1) + k2 delta2
donc deltaprime2 = x2-x1 - delta2

C'est correct ?

[invite742846b3]

la premiere chose a faire est d"etablir les equations du mouvement. Pour tu ecrit les forces qui agissent sur le bloc = masse*acceleration (Merci Newton).
Il y a quatre forces sur le premier (2 ressort, l'amortisseur et le poid) et deux sur le second.
On obtient les equations suivantes :




ou j'ai note C la constante de rappel de l'amortisseur. (Note amortisseur = force proportionelle a la vitesse)

A l'equilibre les derivees par rapport aux temps sont nulles (le systeme n'evolue pas). On obtient alors





d'ou on tire et

Par contre lorsque l'on applique une force sinusoidale, c'est plus complique ! Il faut ajouter cette force dans le membre de droite de la premiere equation (enfin, je crois). Ensuite, tu dois chercher ce qu'on te demande. les accroissements et vont dependre du temps. Si tu cherche la forme analytique exacte, c'est pas evident. Je passerai par la transformee de Laplace qui transforme un systeme d'equations differentiels en un systeme algebrique. Mais tu ne connais pas cette methode et il doit avoir un truc plus simple qu'on t'as enseigne a l'ecole (et que j'ai oublie !)

[invite1d656ca6]

ah oui je comprends merci pour ses explications !
sinon je peux résoudres ces équations différentiels couplés avec la métode des matrice.