bonjojur tt le monde,
c'est un exercice dans la mecanique du point materiel
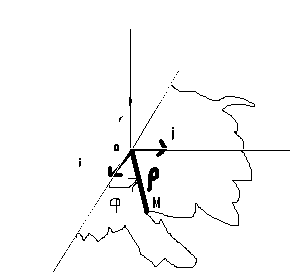
dans la pemiere question j'ai determinet les composantes de v v(ro',rophi',z') et la norme bien sur racine carré de la somme des carrés des composantes ma premiere question : est ce qu'il ya des donnés manquants car je vois qu'on peut pas calculer la norme de vitesseun point materiel M de masse m decrit la trajectoir plane dont l'equation s'ecrit en coordonnées polaire ro=b(1+cosphi) b:constante et phi plus que ou egale 0 et moin strictement de pi
on suppose que l vitesse angulaire=dphi/dt est constante
1-determiner les composantes de la vitesse dans la base cylindrdique et calculer sa norme
2-en deduir la longeur de la trajectoire
3-determinet les composantes de l'acceleration
ma deuxieme question pk on nous demande de determiner les composantes de la vitesse dans la base cylindrdique si la trajectoire est plane donc z=0
ma troisieme question est ce que la longueur de trajectoire c'est le deplacement elementaire dOM ?
-----