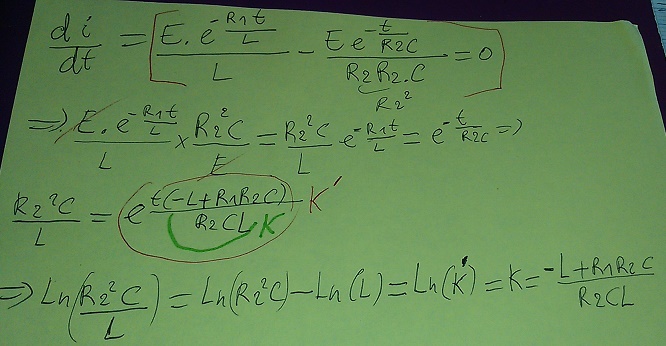Bonjour,j'ai fais cet exercice cependant j'ai euh du mal pour la question 3b),j'aurai besoin d'aide pour cette question si possible.
L'énoncé est le suivant:
On considère un circuit R1L série placé en parallèle à un circuit R2C série.
L'ensemble est alimenté par une source de tension idéale E par l'intermédiaire d'un interrupteur.
1)Réaliser le montage.
2)Le condensateur est initialement déchargé .
A t=0,on ferme l'interrupteur.
Estimeret
circulant dans l'inductance et dans le condensateur pour t>=0(sup ou égal).
3a)puis exprimer i(t) le courant débité par la source.
3)b)calculer le temps t1 pour lequel i(t) est minimum.
A l'aide de t1 et des limites,tracer i(t) en supposant que R1>R2.
Mais voici ce que j'ai fais:
1)Voici le schéma:
102.jpg
2) E = R1.iL + L.diL/dt
iL = K.e^(-R1/L * t) + E/R1
iL(0) = 0 --> K = -E/R1
iL(t) = E/R1 * (1 - e^(-R1/L * t))
E = R2.ic + Uc
avec ic = C.dUc/dt
R2.ic + dUc/dt = 0
R2.dic/dt + ic/C = 0
ic = K'.e^(-t/(RC))
ic(0) = E/R2 --> K' = E/R2
ic(t) = E/R2 * e^(-t/(R2.C))
3) a) i(t) = ic(t) + iL(t)
i(t) = E/R2 * e^(-t/(R2.C)) + E/R1 * (1 - e^(-R1/L * t))
-----