Bonjour,
je cherche mais je ne vois pas mon erreur...
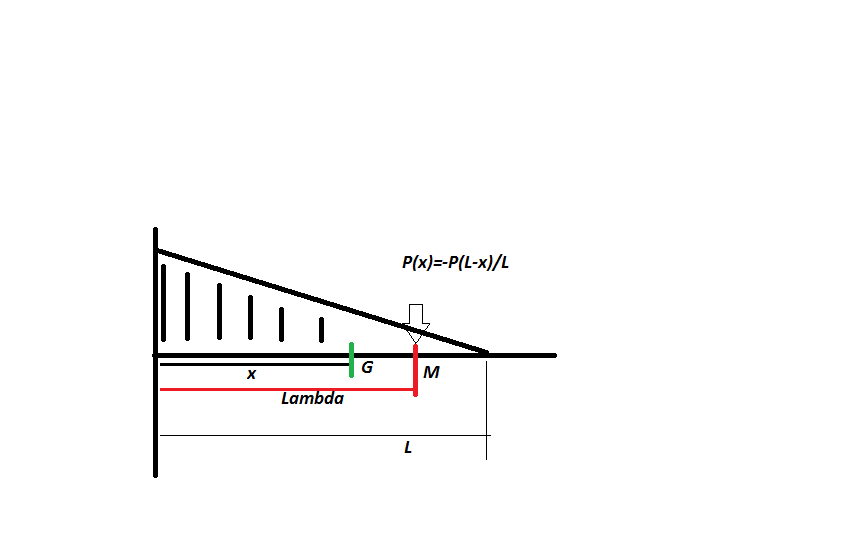
Une poutre console de longueur L avec une charge triangulaire décroissante, je cherche le moment fléchissant.
Une coupure en G et je fais le calcul, je prends à droite comment ça je n'ai pas les réactions à calculer. j'ai ma charge répartie q=-P(L-x)/L en M de distancepar rapport à l'origine que j'intègre entre G (distance x depuis l'origine) et L:
Jusque là c'est bon?
Après j'intègre et je trouve:
or dans les bouquins, je trouve:
J'ai refait les calculs plusieurs fois, impossible de trouver l'erreur, pouvez-vous me débloquer?
Bonne journée.
-----