Problème électrostatique

[ovechkin08]

Bonjour cher lecteur,

j'aurais besoin de savoir ce que je dois réellement trouver en premier pour faire le problème. Le voici:
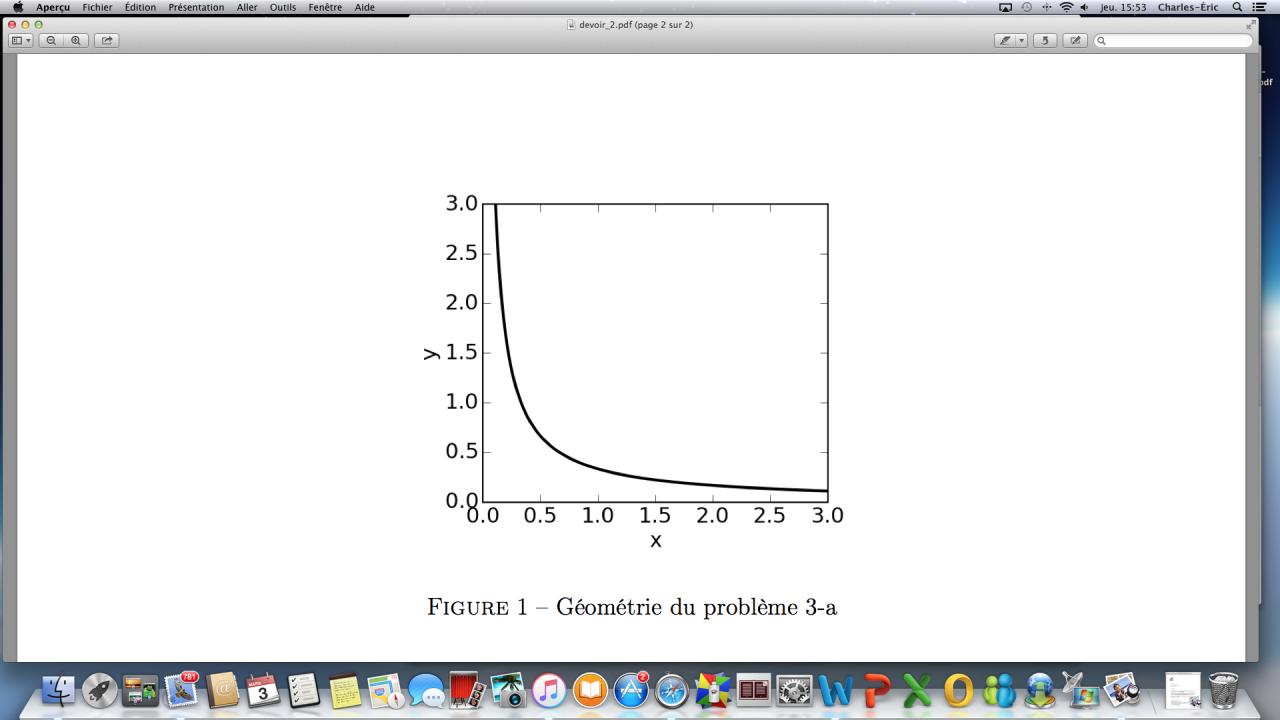
Un conducteur maintenu à un potentiel de 50V dont la forme est décrite par la courbe y = 1/(3x) est placé à proximité d’un coins formé par l’axe x et l’axe y tel qu’illustrée à la figure 1. En sachant que le coin est maintenu à un potentiel de 0, trouvez une expression pour le potentiel dans la région se trouvant entre le coin et le conducteur courbe. Évaluez ce potentiel au point (x = 0.5, y = 0.25).
Figure 1:
Merci beaucoup
-----

[LPFR]

Bonjour.
Où avez-vous trouvé ce problème ?
Car c’est un problème pour adultes.
J’ai retrouvé la méthode : il faut utiliser les fonctions de variable complexe et faire une transformation de Schwarz avec un angle de pi/2.

Après réflexion, je me suis dit qu’il n’est pas possible que l’on vous demande ce type de solution. Il doit donc s’agir d’un problème « à astuce ». Il sufit d’être inspiré et de trouver l’astuce.

On constate que l’équipotentielle donnée est le lieu des points pour x.y = cte. Et que pour ‘x’ ou ‘y’ nuls, xy vaut aussi zéro.

Donc, un tas de fonctions de (x.y) peuvent donner les deux conditions de bord.
Par exemple (x.y)^p ou sinh((x.y)^p).
Mais la fonction doit obéir aux lois de l’électrostatique. Ici c’est le laplacien du potentiel qui doit être nul entre les équipotentielles imposées.

Il ne vous reste qu’à tester toutes les fonctions possibles. Mais je vous conseille de commencer par (x.y)^p
Au revoir.

[ovechkin08]

Bonjour,

en faite j'ai l'impression que l'énoncé se contredit. On a un conducteur avec un potentiel inconstant donc il y a nécessairement un champ électrique à l'intérieur, mais là on ne dit pas qu'il y a une charge donc en supposant qu'il y en a pas le champ devrait être 0 normalement.
C'est un devoir maison alors puisqu'on a le droit à tous le matériel à notre disposition il est certain qu'il demande un peu plus de complexité, mais techniquement il devrait pas être si demandant et je suis quand même à l'Université, mais en effet la formule de Swartch c'est un peu trop pousser, et ce que je sais pour le moment c'est l'équation de Laplace.
Moi j'ai pensé trouvé le champ électrique en supposant qu'il y a une charge inconnu, et j'ai trouvé ce champ partir du potentiel, donc en faisant une dérivée partielle en x et y, mais il semble que je tourne en rond, car si je trouve le champ à partir du potentiel et qu'on demande le potentiel à des points x et y je suis censé faire quoi avec ce champ. -3(x+y)-1 = potentiel =50?? Bref c'est ma version pour commencer le problème. Si vous avez d'autres suggestions n'hésitez pas à me les donner.

Merci

[LPFR]

Bonjour.
Relisez l’énoncé. Les deux conducteurs sont, chacun, à potentiel constant.
Et relisez ce que je vous ai expliqué.
Au revoir.

[A voir en vidéo sur Futura]