Atténuations des vibrations sur un système

[tuyo408]

Bonjour,

Je cherche des pistes sur l'exercice suivant :

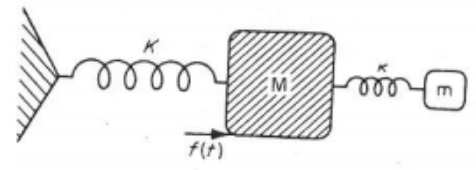
On dispose d'un système d'atténuation représenté sur la figure. La masse M est soumise à une force harmonique f(t)=Fe^(-iwt). On atténue cette masse à l'aide d'un oscillateur de masse m et de raideur k, déterminer k et m pour minimiser les vibrations de la masse M.

Je cherche à établir l'équation du mouvement de M en établissant le bilan des forces s'exerçant sur la masse.
Pour M en x₁ et m en x₂

pour le ressort K: -Kx₁
pour le ressort k: -k(x₁-x₂)
le poids P = Mg
la force harmonique : Fe^(-iwt)

J'ai donc mx₁'' = -Kx₁ - k(x₁-x₂) + Mg + Fe^(-iwt)

Je cherche à savoir si je pars dans la bonne direction en étudiant le mouvement de M..

Merci pour votre aide.



-----

[LPFR]

Bonjour.
Votre méthode consistant à balancer des formules est mauvaise.
Vous avez deux degrés de liberté. Vous devez arriver à deux équations.
Dessinez toutes les forces et leurs points d’application
Écrivez la 2ème loi de Newton pour chacune des masses.

C’est le schéma (incomplet) du système de la Tour de Taipei. Mais tel que vous l’avez dessiné, vous n’aurez aucune atténuation. Il n’y a pas d’élément dissipatif dans l’ensemble. Dans la Tour de Taipei, il y a des amortisseurs entre la masse principale et le pendule en hauteur.

Regardez:
http://forums.futura-sciences.com/ph...de-taipei.html
Au revoir.

[tuyo408]

Ok merci beaucoup de m'avoir éclairé sur ce point, merci !