Célérité de la lumière

[Gohan.]

Bonjour, j'avais un exercice que m'a pris tout mon temps mais que je n'ai toujours pas réussi à faire:
Une roue dentée porte à sa périphérie N=100 dents carrées séparées par des intervalles vides égaux aux dents. Cette roue est entraînée par un moteur dont on peut régler et stabiliser la vitesse à la valeur désirée.
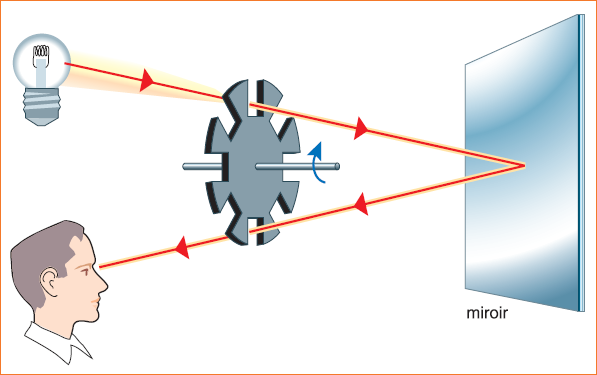
Un arc électrique muni d'un condensateur est placé à la périphérie de la roue, de telle manière que sa lumière soit occultée lorsqu'une dent passe devant l'axe du condensateur, et puisse passer librement lorsqu'un intervalle se trouve devant cet axe. On obtient ainsi de bref éclair qui se propagent jusqu'au miroir M, qui les renvoie sur la roue. La distance séparant la roue du miroir est D=11,5 km.
L'observateur O vise le miroir à l'aide d'une lunette L placée à la périphérie de la roue, de telle manière que son objectif puisse être alternativement occulté et découvert par les dents et les intervalles.
A l'instant t=0 l'arc et la lunette commencent simultanément à se découvrir, un intervalle s'engageant devant chacun d'eux. La vitesse de rotation de la roue n tours/s et l'on désigne par C la vitesse de la lumière dans l'air.
1. Exprimer en fonction de d,n,N et d'un entier k,les intervalles de temps où l'arc électrique et la lunette sont simultanément démasqués, et les intervalles où ils sont occultés par les dents de la roue.
En fait c'est la seule question qui me pose problème dans tout l'exercice (surtout le "d" que j'ignore ce que ça représente donc un problème pour l'introduire dans mon expression), les autres questions n'étant pratiquement pas liées à celle-ci.Merci de votre aide
-----

[mach3]

Le "d" ne peut être que la distance "D" de 11,5km. Une faute de frappe sans doute.

m@ch3

[Gohan.]

Bonjour, voilà mes réponses:
l'arc et la lunette sont simultanément démasqués par θ= 2k D.(N+1) /n et simultanément occultés pour θ= 2k D.N /n car au départ l'arc et la lunette commencent simultanément à se découvrir. Merci de vérifier si c'est bon.

[mach3]

Je n'ai pas bien réfléchi avant de vous répondre, d ne peut pas être la distance D, ça n'a aucun sens (je n'ai pas bien lu la question et du coup pas bien compris ce qui était demandé...). Je ne vois pas ce que peut être d, vu que la réponse que je trouve ne dépend que de k, N et n. Il y a quelque chose qui manque dans l'énoncé.
Je vous explique quand même ce que j'ai trouvé (moyennant ce que je crois comprendre de l'exercice). La roue fait un tour complet en 1/n secondes. Elle a N dents
En 1/2N de tour, un trou est remplacé par la dent suivante,
en 2/2N de tour, un trou est remplacé par le trou suivant,
en 3/2N de tour, un trou est remplacé par la dent qui suit la dent suivante,
en 4/2N de tour, un trou est remplacé par le trou qui suit le trou suivant... etc

bref en (2k+1)/2N de tour, il y a occultation et en 2k/2N=k/N de tour, il n'y a pas occultation. La durée entre le passage d'un trou et de la dent qui le suit est donc 1/2Nn, et entre un trou et n'importe quelle dent, (2k+1)/(2Nn). La durée entre le passage d'un trou et du trou qui le suit est 2/2Nn, et entre un trou et n'importe quelle autre 2k/2Nn=k/Nn. Pour vérifier, regardons le temps qui s'écoule entre deux passages du même trou, on a k=N, donc le temps est 1/n, la durée d'une rotation complète de la roue.

Je ne vois vraiment pas ce que peut être d, il semble qu'on n'en ait pas besoin pour répondre.
Il est possible que dans une autre version de l'exercice, on ne donne pas la vitesse de rotation en tour/sec, mais la vitesse de la périphérie en m/s, ce qui exigerait donc de connaitre le diamètre (souvent noté d) pour connaitre le nombre de tour/sec. Il y a peut-être eu une omission en modifiant l'exo.
Une autre possibilité que je vois est que la lunette et l'arc électrique ne donnent pas sur le même trou (ce que j'ai considéré par défaut, vu que cela n'est pas précisé), mais sur deux trous distants de d

m@ch3

[A voir en vidéo sur Futura]

[Gohan.]

En fait l'exercice est accompagné d'une image ressemblant à celle ci dessous:
Donc on voit bien que la lunette et l'arc électrique ne donnent pas sur le même trou.
Est-ce que cela n'influerait pas sur mon expression?

[LPFR]

Bonjour.
Oui. Si ce n’est pas el même trou, ou si la lumière est arrêtée au retour pendant qu’elle peut sortir, cela changerait (un peu) votre formule.
Mais ce qui ne changera pas est le fait qu’entre deux vitesses consécutives permettant de voir la lumière, il y a une dent de différence dans la rotation de la roue. Et que cette différence de temps correspond à l'aller retour de la lumière.
Mais, au niveau de l’exercice, cela ne changera rien (à part la formule). Vous pouvez le faire comme si le trou de départ et d’arrivée était le même.

Nota : je suppose que vous savez que cette expérience de mesure de la vitesse de la lumière est connue comme « expérience de Fizeau ».
Au revoir.

[phys4]

Bonsoir tous,
Il me semble que personne n'a pris en compte le temps d'aller-retour de la lumière t = 2D/C
Ce temps doit correspondre a un nombre entier de périodes de la structure de la roue dentée = 1/Nn
soit pour que la lumière soit visible
2D/C = k/Nn et donc
n = k* C/(2DN)
Pour éteindre la lumière il faut un nombre entier plus une demi période de la roue dentée soit :
2D/C = (2k +1)/(2Nn) car il y a 2N demi périodes par tour
n = (2k + 1)*C /(4DN)

Au revoir.

[mach3]

Il me semble que personne n'a pris en compte le temps d'aller-retour de la lumière t = 2D/C

j'ai pensé qu'il fallait le faire au début, mais en relisant la question, il me semble que ce n'est pas ce qui est demandé :

Exprimer en fonction de d,n,N et d'un entier k,les intervalles de temps où l'arc électrique et la lunette sont simultanément démasqués, et les intervalles où ils sont occultés par les dents de la roue.

on demande un intervalle de temps

Ce n'est qu'après qu'on met en relation l'intervalle de temps avec le temps d'aller retour de la lumière.

m@ch3

[Gohan.]

Bonsoir, je pensais même que mon poste avez été oubliée. J'ai bien lu vos suggestions et je pense avoir compris le problème. Merci encore vous m'avez bien aidé.