Oscillateur harmonique amorti et dirac

[vtyr]

Bonjour à tous,

Je suis en train d'essayer d'établir l'équation du mouvement d'un oscillateur harmonique amorti (masse, ressort et amortisseur).
Les conditions initiales serait un position et une vitesse nulle mais on lui applique une force Fo (un dirac en fait).

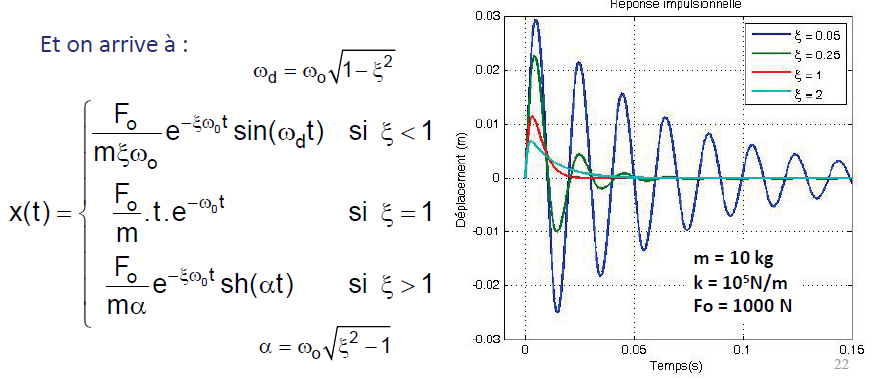
J'ai trouvé sur internet un PDF qui donnait la solution suivante:


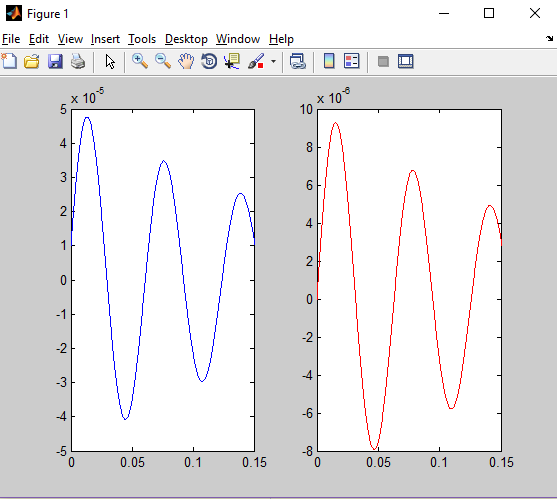
J'ai essayé de tracer l'équation avec un xi<1 (ce qui correspond à mon système) avec bien sur les valeurs qui sont indiqué sur le graphique...
Et je ne tombe pas sur le même graph que lui...
Est ce que sa formule est fausse??

Merci de votre aide
-----

[albanxiii]

Bonjour et bienvenu sur le forum,

Quelle formule trouvez-vous ?
Pouvez-vous poster vos calculs ?

@+

[vtyr]

Bonjour,

Pour ma part, j'ai effectué une résolution classique de l'équation Mx''+Cx'+Kx=0 avec pour conditions initiales x(0)=F0/k et x'(0)=0. (k étant la raideur du ressort et c l'amortissement).

Je trouve au final la solution suivante:
x(t)=(F0/(K)).*((exp(-xi*w0*t).*(cos(wd*t)+xi*w0*sin (wd^2)*t))))

avec :
w0=sqrt(K/M)
wd=w0*sqrt(1-(xi^2))
C=2*M*w0*xi

Je trace avec matlab l'équation que trouve, et celle qui est indiqué dans le PDF et je trouve deux résultats différents...



La courbe bleue représente le graphique obtenue avec l’équation du PDF et la rouge celle obtenue avec mon équation. De plus, aucune ne correspond a la courbe du PDF...

Je me pose donc des questions sur la véracité de la courbe du PDF et j'aimerais également savoir quelle solution est la bonne... Il doit surement y'avoir un problème dans les conditions initiales...

Merci de votre aide

[vtyr]

Bonjour,
Est ce quelqu'un connait l'équation d'un oscillateur harmonique amorti avec les conditions initiales nulles auquel on applique un dirac?

Merci

Les doublons sont interdits. Merci.

[A voir en vidéo sur Futura]

[LPFR]

Bonjour
Vos conditions initiales sont fausses.
S’il la masse a reçu une impulsion de Dirac à t = 0, sa vitesse dévient instantanément non nulle mais sa position initiale reste inchangée à 0.
Au revoir.

[coussin]

La courbe bleue représente le graphique obtenue avec l’équation du PDF et la rouge celle obtenue avec mon équation. De plus, aucune ne correspond a la courbe du PDF...

Y a qu'un facteur constant entre les deux, non ?